Геометрическая Волновая Инженерия: Псевдогиперболоиды

1.1. Введение в геометрическую волновую инженерию (ГВИ)

Геометрическая волновая инженерия (ГВИ) представляет собой революционное междисциплинарное направление в современной науке и технике, которое фундаментально меняет подход к управлению волновыми процессами. ГВИ ставит во главу угла геометрию пространства. Здесь форма не является пассивным носителем, а становится активным инструментом, способным программировать траектории волн, фокусировать энергию и создавать эффекты, недостижимые в классических системах.

ГВИ возникла как ответ на ограничения существующих технологий: высокие потери энергии, сложность производства материалов и необходимость в активных элементах (например, электронике для фазированных антенн).

Авторское предложение этого направления подчеркивает, что искривление пространства – это универсальный ключ к управлению волнами любой природы. Основой ГВИ служат псевдоповерхности с переменной отрицательной кривизной, которые позволяют экспоненциально расходящимся геодезическим линиям (кратчайшим путям волн) превращаться в контролируемые потоки. Это не просто теория: современные методы, такие как 3D-печать, нанофабрикация и компьютерное моделирование, делают ГВИ практически реализуемой.

1.2. Открытие «псевдоповерхностей»

В рамках геометрической волновой инженерии были открыты уникальные геометрические формы, названные «псевдоповерхностями», такие как псевдопараболоиды, псевдогиперболоиды и псевдоэллипсоиды. Приставка «псевдо» используется для того, чтобы подчеркнуть их отличие от классических фигур, изучаемых в математике.

Псевдоповерхности – это класс геометрических объектов, характеризуемых переменной отрицательной гауссовой кривизной. ГВИ утверждает, что эти поверхности не существуют изолированно, они являются проявлением единой парадигмы, где геометрия диктует поведение волн. Все псевдоповерхности – от псевдопараболоидов и псевдогиперболоидов до псевдоэллипсоидов и высших порядков – строятся на принципах ГВИ.

Единая схема построения: Псевдоповерхности формируются путем зеркального копирования базового профиля (параболического, гиперболического или эллиптического) и его вращения вокруг смещенной оси. Это создает локальные структуры, где волны не фокусируются в точку (как в положительной кривизне), а локализуются в областях, циркулируют или задерживаются. ГВИ объединяет эти конструкции, показывая, как изменение параметров (смещение R, порядок вращения) позволяет "программировать" волновые эффекты.

Физическая основа: В ГВИ отрицательная кривизна вызывает экспоненциальное расхождение геодезических линий, но при правильном дизайне это приводит к эффектам, аналогичным "волновым ловушкам" или "геометрическим черным дырам". Все псевдоповерхности наследуют эти свойства, делая ГВИ фундаментом для их классификации и применения.

Классификация в ГВИ: Псевдоповерхности делятся по видам (по образующей: параболические, гиперболические, эллиптические) и типам (порядкам: 2-го – одинарное вращение, 3-го – двойное, и выше). ГВИ объясняет, почему высшие порядки вводят замкнутые области, усиливая эффекты, такие как эргодические моды (равномерное распределение волн).

Без ГВИ псевдоповерхности остались бы абстрактными математическими конструкциями. ГВИ превращает их в инструменты для реального мира.

1.3. ГВИ как новое направление в науке и технике

ГВИ – это не эволюция существующих дисциплин, а принципиально новое направление, интегрирующее дифференциальную геометрию, волновую физику, материаловедение и инженерию. Оно возникло в контексте поиска энергоэффективных решений для XXI века, где традиционные подходы достигли пределов (например, дифракционный предел в оптике или потери в метаматериалах).

Научные аспекты: ГВИ открывает двери к изучению нелинейных волновых явлений в искривленных пространствах, аналогов релятивистской физики (например, эффекты, подобные горизонту событий). Это связывает ГВИ с квантовой гравитацией, AdS/CFT-теорией и гиперболической геометрией. В астрономии – фокусировкой гравитационных волн.

Технические применения: ГВИ революционизирует отрасли:

Телекоммуникации: Компактные антенны для ТГц-связи без потерь.

Энергетика: Солнечные концентраторы без слежения, беспроводная передача энергии, Ядерный синтез и т.п.

Медицина: Неинвазивные сканеры с многозонной фокусировкой.

Оборона: Невидимые экраны и направленные излучатели.

Квантовая инженерия: Резонаторы для квантовых компьютеров.

Перспективы развития: Как новое направление, ГВИ требует междисциплинарных исследований. Будущие работы включают интеграцию с ИИ для оптимизации геометрии и эксперименты с метаматериалами для реализации на наноуровне

В заключение, ГВИ – это мост от теории к практике, где псевдоповерхности становятся универсальными инструментами. Эта глава закладывает фундамент для понимания серии книг, посвященных конкретным реализациям.

2.1. От пассивной формы к активной функции

Человечество веками училось управлять волнами, будь то свет, звук или радиосигнал, преимущественно через свойства материала. Линзы из стекла, антенны из металла, метаматериалы с экзотическими диэлектрическими свойствами – все эти инструменты основывались на представлении о том, что материал определяет путь волны. Но что, если сам путь – сама геометрия пространства – может стать главным инструментом управления?

Геометрическая волновая инженерия (ГВИ) предлагает радикально новую концепцию. Это междисциплинарное направление, где управление волновыми процессами достигается не за счёт изменения материальных свойств, а за счёт искривления пространства, по которому распространяется волна. В этом подходе геометрия, которая раньше считалась пассивным фоном, превращается в активный компонент, способный фокусировать, направлять и даже удерживать энергию.

Основой геометрической волновой инженерии являются псевдоповерхности с переменной отрицательной кривизной.

Такие поверхности с переменной отрицательной кривизной представляют собой новый класс геометрических объектов, обладающий рядом уникальных физических свойств, которые открывают совершенно новые возможности в различных научных дисциплинах и технических приложениях.

Прежде всего, стоит отметить характерные признаки таких поверхностей:

Форма поверхности. Любая точка внутри поверхности имеет различную отрицательную кривизну.

Применение. Благодаря своей структуре, поверхности с отрицательной кривизной проявляют замечательные свойства в обработке и контроле волн разной природы (свет, звук, электромагнитные поля).

В ГВИ эти поверхности становятся "волновыми программистами". Они задают траектории геодезических линий – кратчайших путей для волн, которые расходятся экспоненциально, создавая эффекты локализации, замедления или даже аналогов чёрных дыр. Это не фантастика, современные технологии, как 3D-печать и нанофабрикация, позволяют воплотить такие формы в реальность, открывая двери для энергоэффективных устройств в медицине, телекоммуникациях и даже квантовых вычислениях. Переход от пассивной формы к активной функции – это как эволюция от простого зеркала к умному зеркалу, которое само решает, куда отразить свет.

2.2. Псевдоповерхности переменной отрицательной кривизны

В отличие от поверхностей с положительной кривизной, которые собирают лучи в одну точку, псевдоповерхности с переменной отрицательной кривизной вызывают экспоненциальное расхождение геодезических линий (кратчайших путей для волн). Но при правильном проектировании это расхождение можно контролировать, создавая уникальные эффекты, недостижимые в классической оптике и акустике.

Давайте разберёмся, что такое отрицательная кривизна на простом примере.

Представьте седло: в одной плоскости оно изгибается вверх, в другой – вниз. Это и есть отрицательная гауссова кривизна (K < 0), где главные кривизны имеют противоположные знаки. В псевдоповерхности волны не фокусируются в точку, как в сферической линзе, а создают области локализации, где энергия задерживается или циркулирует без границ.

Это приводит к потрясающим эффектам: волновые ловушки, где свет или звук "застревает" без отражателей; безлинзовая фокусировка, снижающая искажения; геометрическая защита, где сигнал не выходит за пределы траектории. В ГВИ псевдоповерхности – это не просто формы, а инструменты для пространственно-программируемых структур, где кривизна "запрограммирована" для фильтрации, усиления или демультиплексии. С помощью метаматериалов и нанотехнологий мы можем создавать такие поверхности на микроуровне, превращая абстрактную геометрию в реальные устройства – от ТГц-волноводов для сверхбыстрой связи до аналогов чёрных дыр для накопления энергии. Это переход к управления волнами через форму пространства, где геометрия становится активным игроком.

2.3. Виды псевдоповерхностей

Существуют 3 основных вида псевдоповерхностей переменной отрицательной кривизны.

К ним относятся:

Псевдопараболоид.

Псевдогиперболоид.

Псевдоэллипсоид.

Классификация псевдоповерхностей по видам основана на особенностях их образующих:

Псевдопараболоиды имеют образующую – сегментпараболы.

Псевдогиперболоиды имеют образующую – сегмент гиперболы.

Псевдоэллипсоиды имеют образующую – сегмент эллипса.

Каждая из этих поверхностей сохраняет ключевые принципы нелокальной геометрии гиперболических (K < 0) структур, но дополнительно вводит асимметрию, масштабируемость и возможность вариативного управления геодезическими траекториями.

В контексте ГВИ эти виды – как разные инструменты в арсенале инженера. Эти поверхности не существуют глобально в евклидовом пространстве, но локально их можно реализовать через метаструктуры, открывая применения от медицинской диагностики (точная фокусировка ТГц-волн) до обороны (невидимые экраны).

2.4. Типы (порядок) псевдоповерхностей

Исходя из классического определения – порядок фигуры показывает степень её описания в математике. Фигуры первого порядка (например, прямая линия) описываются простыми линейными уравнениями. А вот фигуры второго порядка, такие как эллипс, окружность, гипербола и парабола, требуют квадратных уравнений для своего точного представления.

Теперь перейдём к псевдоповерхностям.

Тип псевдоповерхностей определяется таким же порядком, или по простому – способом построения.

Одинарное вращение образующего профиля вокруг оси, параллельной оси симметрии, но смещенной от него на R формирует псевдоповерхности 2-го порядка

Двойное вращение образующего элемента вокруг оси, параллельной оси симметрии, но смещенной от него на R формирует псевдоповерхности 3-го порядка.

В ГВИ типы псевдоповерхностей – это как этажи в здании сложности. Порядок определяет, насколько многофункциональными станут траектории волн. Одинарное вращение создаёт 2-й порядок – относительно простую структуру, но уже с переменной кривизной, где геодезические линии формируют устойчивые моды, как в резонаторе без границ. Двойное вращение поднимает на 3-й порядок, вводя дополнительные замкнутые.

Аналогия: если 2-й порядок – как простая воронка, собирающая дождь в ведро, то 3-й – как лабиринт воронок, где вода циркулирует, накапливаясь в нескольких резервуарах.

2.5. Псевдоповерхности 2-го порядка

Все псевдоповерхности 2-го порядка строятся по единой схеме. Берется базовый профиль (например, параболический, гиперболический, эллиптический, круглый). Он зеркально копируется и может раздвигаться на некоторое расстояние по оси фокусов. Полученная фигура вращается вокруг новой оси, параллельной оси фокусов и смещенной на R. Таким образом формируются псевдоповерхности второго порядка.

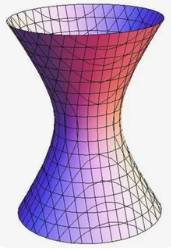
Рис. № 1. Образующий профиль псевдоповерхностей 2-го порядка.

Визуально псевдоповерхности 2-го порядка представляют собой две перевёрнутые воронки, соединённые основаниями, или имеют небольшой зазор. Имеют переменную отрицательную кривизну стенок.

В ГВИ псевдоповерхности 2-го порядка – это "стартовый уровень" революции, где простая схема вращения рождает сложные эффекты. Возьмём базовый профиль, зеркально скопируем его – и вот у нас симметричная форма, которую мы вращаем вокруг смещённой оси. Результат: поверхность, напоминающая две соединённые воронки, с кривизной, меняющейся от точки к точке, создавая гиперболическую геометрию локально. Волны здесь не просто отражаются – они "программируются" на задержку, фокусировку в области или циркуляцию, как в волновой ловушке без стен. Такие поверхности идеальны для ТГц-диапазона: они позволяют создавать компактные антенны или сенсоры, где геометрия заменяет сложные материалы, снижая потери и повышая эффективность. В практике это открывает двери для новых подходов в безопасности (направленные детекторы) и бионике (имитация природных навигаторов), делая 2-й порядок фундаментом для повседневных инноваций.

2.6. Псевдоповерхности 3-го порядка

Псевдоповерхности третьего порядка представляют собой дальнейшее развитие идей геометрической волновой инженерии, выходящее за рамки классических и обобщённых поверхностей второго порядка.

Они создаются так. Берется поперечное сечение псевдоповерхности второго порядка, полученное вращением образующей вокруг оси симметрии. Такое сечение похоже на четырёхконечную звезду с вогнутыми по законам окружности или параболы, или гиперболы или эллипса гранями. И вращается вокруг новой оси, сдвинутой на определённую величину относительно оси вращения псевдоповерхности 2-го порядка.

Рис. № 2. Образующий профиль псевдоповерхностей 3-го порядка.

Псевдоповерхности 3-го порядка – это объекты, сформированные путём комплексного преобразования базовой поверхности путём повторных операций вращения и трансформации исходных форм (трактрисы, гиперболы, параболы или эллипса). Основополагающим отличием этих поверхностей является образование нескольких замкнутых областей внутри объема, что кардинально отличает их от стандартных поверхностей 2-го порядка.

В ГВИ псевдоповерхности 3-го порядка – это "высший пилотаж", где создаётся многомерная топология с замкнутыми областями, похожими на внутренние "комнаты" в лабиринте. Берем сечение 2-го порядка – эту "звезду" с вогнутыми гранями – и вращаем его вокруг смещённой оси, получая структуру с несколькими полостями, где волны могут циркулировать независимо. Аналогия: если 2-й порядок – как простая труба для потока, то 3-й – как сеть труб с перекрёстками, где энергия может "выбирать" пути, формируя сложные интерференционные паттерны.

Цель главы:

Рассмотреть основу всех псевдогиепрболоидов

3.1. Геометрическое определение гиперболы

Гипербола – это геометрическое место точек, для которых абсолютная разность расстояний до двух фиксированных точек (фокусов) постоянна и равна 2a.

Уравнение: (x²/a²) – (y²/b²) = 1 (в каноническом положении, с вершиной в начале координат и осью симметрии вдоль X или Y)

Где:

a – расстояние от центра до вершины (полуось),

b – параметр, связанный с асимптотами (b² = c² – a², где c – расстояние от центра до фокуса).

Ключевая особенность: гипербола обладает двумя фокусами F1 и F2 и двумя асимптотами (в отличие от эллипса или параболы).

3.2. Фокальный закон гиперболы

Любой луч, направленный к одному фокусу гиперболы, после отражения от её вогнутой стороны отражается так, будто он исходит из другого фокуса.

И наоборот: любой луч, выпущенный из одного фокуса, после отражения направляется к другому фокусу.

Рис. № 3. Фокальный закон гиперболы

Это уникальное свойство и есть причина популярности гиперболических форм в отражающей технике.

Математически это следует из равенства углов падения, отражения и кривизны поверхности, исходя из уравнения гиперболы.

В контексте ГВИ этот классический закон приобретает новую, динамическую интерпретацию. Вместо использования одного отражения для фокусировки, ГВИ-системы масштабируют этот принцип на сложную, замкнутую структуру с несколькими фокусами, заставляя волны совершать многократные отражения. Это позволяет управлять траекторией луча через серию последовательных отражений, а не через одну фокусную точку, что приводит к формированию более сложных и устойчивых волновых полей. Таким образом, ГВИ преобразует статический фокальный закон в динамическое, многоотражательное поведение.

Цель главы:

Показать, как из половинки вертикальной гиперболы можно построить замкнутую симметричную 2D-фигуру, сочетающую в себе многократные фокусные направления – первую реализацию концепции геометрической волновой инженерии, как 2D псевдогиперболоид 2-го порядка.

4.1. Геометрия фигуры

Построение: