Brückenkurs Statistik für Wirtschaftswissenschaften

- -
- 100%
- +


Eine Arbeitsgemeinschaft der Verlage
Böhlau Verlag · Wien · Köln · Weimar
Verlag Barbara Budrich · Opladen · Toronto
facultas · Wien
Wilhelm Fink · Paderborn
A. Francke Verlag · Tübingen
Haupt Verlag · Bern
Verlag Julius Klinkhardt · Bad Heilbrunn
Mohr Siebeck · Tübingen
Nomos Verlagsgesellschaft · Baden-Baden Ernst Reinhardt Verlag · München · Basel
Ferdinand Schöningh · Paderborn
Eugen Ulmer Verlag · Stuttgart
UVK Verlagsgesellschaft · Konstanz, mit UVK/Lucius · München
Vandenhoeck & Ruprecht · Göttingen · Bristol
Waxmann · Münster · New York
Peter von der Lippe
Brückenkurs
Statistik für
Wirtschaftswissenschaften
Was Sie vor Vorlesungsbeginn wissen sollten
UVK Verlagsgesellschaft mbH · Konstanz
mit UVK/Lucius · München
Autorenangaben
Prof. Dr. Peter von der Lippe lehrte an der Universität Essen.

Lösungen der Verständnisfragen sowie weitere Übungsfragen finden Sie online unter www.uvk-lucius.de/brueckenkurse.

Die Deutsche Bibliothek – CIP Einheitsaufnahme
Die Deutsche Nationalbibliothek verzeichnet diese Publikation in der Deutschen Nationalbibliographie; detaillierte bibliographische Daten sind im Internet über
Das Werk einschließlich aller seiner Teile ist urheberrechtlich geschützt. Jede Verwertung außerhalb der engen Grenzen des Urheberrechtsgesetzes ist ohne Zustimmung des Verlags unzulässig und strafbar. Das gilt insbesondere für Vervielfältigungen, Übersetzungen, Mikroverfilmungen und die Einspeicherung und Verarbeitung in elektronischen Systemen.
© UVK Verlagsgesellschaft mbH, Konstanz und München 2015
Lektorat: Rainer Berger
Gestaltung: Claudia Rupp, Stuttgart
Illustrationen: © dragonstock – fotolia.com
Einbandgestaltung: Atelier Reichert, Stuttgart
UVK Verlagsgesellschaft mbH
Schützenstraße 24 · 78462 Konstanz
Tel. 07531-9053-0 · Fax 07531-9053-98
www.uvk.de
UTB-Band-Nr.: 4333
E-Book ISBN 978-3-8463-4333-3
eBook-Herstellung und Auslieferung:
Brockhaus Commission, Kornwestheim
www.brocom.de
Inhalt
1Was ist Statistik?





Wichtige Begrifflichkeiten
Gesamtheit: Eine Zusammenfassung von Einheiten (Elementen), bei denen Merkmale erhoben werden und die somit Gegenstand einer Statistik ist.
Merkmale: Sie werden mit x oder y bezeichnet. Der bei Einheit i beobachtete (gemessene, oder allgemein „erhobene“) Wert bezüglich der Variable x ist xi. Ein Merkmal ist durch seine Merkmalsausprägungen (im Falle des Merkmals Geschlechts: männlich und weiblich), bzw. möglichen Messwerte oder einfach „Werte“ definiert. Merkmale werden auch Variablen genannt.
Stichprobe: Die Stichprobe ist eine Teilerhebung, wenn die Einheiten aus der „Grundgesamtheit“ nach dem Zufallsprinzip ausgewählt werden.
Statistik: Die Statistik ist (1.) eine Wissenschaft, (2.) eine empirische Untersuchung (ein entsprechender Text mit Tabellen, Graphiken usw.) und (3.) eine Kennzahl auf Basis von Stichprobendaten.
Die Statistik begegnet Ihnen in vielen Bereichen des täglichen Lebens. Denken Sie nur an Ihre Semesterarbeit, in der Sie statistisches Datenmaterial auswerten müssen, oder an Glücksspiele wie zum Beispiel Würfeln oder Lotto.
Sie ist die Lehre der Methoden zur Gewinnung und Analyse von zahlenmäßigen Informationen über die Wirklichkeit. Diese Informationen stammen aus der Befragung, Beobachtung oder Messung von
■Merkmalen (z. B. Alter, Einkommen etc.) an■Einheiten (z. B. Personen, Betriebe oder auch Objekte wie z. B. Wohnungen)■einer statistischen Masse (Gesamtheit).Statistiker sammeln also Informationen und werten sie aus. Wissenschaftlich ausgedrückt erheben sie Daten über eine Gesamtheit, Teilgesamtheit oder speziell eine Stichprobe – letztere wird nach dem Zufallsprinzip ausgewählt. Sie tun dies, indem sie feststellen, welche Merkmalsausprägungen bzw. welche Messwerte bei einer Einheit vorliegen.
Beispiele für Merkmalsausprägungen in der Statistik
Das Alter x nimmt bei Person i den Wert xi = 21 Jahre an. Oder: Der Umsatz eines Unternehmens liegt in der Größenklasse zwischen 150.000 und 200.000 €.
Das Ziel der Statistik ist es, Aussagen über „Massen“ in Bezug auf Merkmale (Variablen) zu machen und zu prüfen, ob derartige Feststellungen, wenn sie aufgrund einer Stichprobe gewonnen wurden, verallgemeinerungsfähig sind. Diese Massen sind hinsichtlich sachlicher, räumlicher und zeitlicher Kriterien sinnvoll gebildete Gesamtheiten.

Verständnisfragen
Haben Sie alles verstanden? Mit den folgenden Fragen können Sie das Gelernte schnell prüfen:
1Ergänzen Sie den Satz:Die Statistik ist die Lehre der Methode zur_______________ und ________________ von zahlenmäßigen Informationen über die Wirklichkeit.
2Was untersuchen StatistikerInnen nicht?□Merkmale□Beschreibung einer einzelnen Einheit□statistische Masse (Gesamtheit)3Was ist kein Merkmal?□Alter□Einkommen□eine einzelne Person P4Wo verfährt man nach dem Zufallsprinzip? Bei der …□Auswahl der Einheiten der Grundgesamtheit im Falle einer Stichprobe□Befragung einer wie immer bestimmten Teilgesamtheit (z. B. der zufällig anwesenden Hörer einer Vorlesung)
Die Lösungen finden Sie online unter www.uvk-lucius.de/brueckenkurse
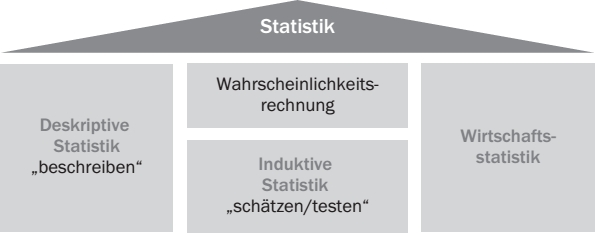
Abb. 1: Die Statistik im Überblick
Die Statistik lässt sich in
■die Beschreibende bzw. Deskriptive und■die Schließende bzw. Induktive Statistikunterscheiden. An einigen Hochschulen wird auch noch Wirtschaftsstatistik gelehrt.
Deskriptive Statistik
Bei der Deskriptiven Statistik geht es um die Gewinnung aussagekräftiger Maßzahlen, wie z. B.
■Mittelwerte,■Streuungsmaße,■Indexzahlen,■Korrelationskoeffizienten usw.Diese Maßzahlen helfen dabei, einen Datensatz sinnvoll zu beschreiben und zu charakterisieren. Mittelwerte kennzeichnen die Größenordnung oder das Niveau, in der bzw. auf dem sich die einzelnen Werte bewegen.
Beispiel für Mittelwerte
Ein Mittelwert
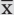
Da es in der Regel Abweichungen nach oben oder unten gibt, sollte nicht nur ein Mittelwert, sondern auch die Streuung gemessen werden. Dabei hilft die Varianz
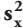
In der Deskriptiven Statistik spielt es keine Rolle, ob die Daten für die Berechnung einer Maßzahl (wie z. B. der oben genannte Mittelwert

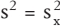
Statistiker sprechen von einer Vollerhebung, wenn die gesamte Grundgesamtheit untersucht wird. Das ist zum Beispiel der Fall, wenn ohne Ausnahme alle Absolventen eines Jahrgangs zu einem Thema befragt werden. Eine Teilerhebung – insbesondere wenn die Einheiten nach dem Zufallsprinzip ausgewählt wurden – liegt vor, wenn lediglich eine Stichprobe aus der Grundgesamtheit befragt wird, also zum Beispiel nur 25 von 1.000 Absolventen befragt werden.
Im Zusammenhang mit Stichproben ist es üblich, griechische Buchstaben zu verwenden, wie zum Beispiel μ oder σ; lassen Sie sich davon nicht abschrecken.
Aber berücksichtigen Sie im Hinblick auf die Induktive Statistik das Folgende: In der Induktiven Statistik müssen Sie durch Symbole unterscheiden, ob sich etwas auf die Grundgesamtheit oder auf die Stichprobe bezieht. Um hier Klarheit zu schaffen verwenden Statistiker
■lateinische Buchstaben (z. B. Standardabweichung s) wenn es sich um die Stichprobe handelt und■griechische Buchstaben (Standardabweichung der Grundgesamtheit σ) wenn die Grundgesamtheit gemeint ist.Induktive Statistik
Bei der Induktiven Statistik geht um die Beurteilung einer Maßzahl (etwa
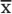
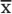
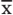

Eine Hypothese ist in der Statistik eine Annahme über die Grundgesamtheit, die durch Daten der Stichprobe geprüft werden kann.
Beispiel Prüfung einer Hypothese
Die Wirkung von Schlankheitspillen kann durch zwei Gruppen getestet werden: Die erste Stichprobe (Experimentgruppe) nimmt die Pillen ein und eine zweite Stichprobe (Kontrollgruppe) nicht. Nach der Einnahme zeigt sich, dass die durchschnittliche Gewichtsabnahme
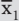
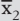
Sie sind der Meinung, dass die Pillen wirken? Vorsicht: Dadurch ist noch nicht bewiesen, dass die Pillen tatsächlich gewirkt haben, denn
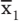
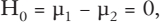
und sie stellen sich die Frage, wie wahrscheinlich
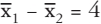
Dieses Beispiel zeigt, dass bei Stichproben immer ein Auswahlfehler vorliegt. Aber dieser Auswahlfehler ist ein Zufallsfehler, weil der Stichprobe eine Zufallsauswahl zugrunde liegt. Auf ihn, und damit auch auf das Schätzen und Testen sind die Regeln und Sätze der Wahrscheinlichkeitsrechnung anwendbar. Die Wahrscheinlichkeitsrechnung ist deshalb auch die theoretische Grundlage für die Induktive Statistik.
Wirtschaftsstatistik
Neben der Deskriptiven und der Induktiven Statistik gibt es ein drittes Teilgebiet der Statistik – die Wirtschaftsstatistik (Wirtschafts- und Sozialstatistik), die heute allerdings im Bachelorstudium oft nicht mehr gelehrt wird. Sie widmet sich der Analyse der begrifflichen und methodischen Grundlagen der Daten der amtlichen Statistik. Dazu zählt z. B. die Berechnung von Sterbetafeln (woraus sich die Lebenserwartung ergibt), der Arbeitslosenquote, des Kapitalstocks, des Inlandsprodukts usw. oder die Bestimmung von Indizes, wie ein Verbraucherpreis-, Auftragseingangs- oder Produktionsindex.

Verständnisfragen
Haben Sie alles verstanden? Mit den folgenden Fragen können Sie das Gelernte schnell prüfen:
1Was ist kein Teilbereich der Statistik?□Deskriptive Statistik□Analyse der Eigenschaften einer einzelnen Einheit (z. B. der Person P)□Induktive Statistik2Was bedeutet deskriptiv?□beschreiben□erklären□vorhersagen3Was berechnet die deskriptive Statistik nicht?□Mittelwerte□Korrelationen□Auswahlfehler4)Ergänzen Sie den Satz:Zentrale Gegenstände der induktiven Statistik sind das____ _______________ von Parametern und das_______________ von Hypothesen über Parameter.
5Was ist ein Gegenstand der Wirtschaftsstatistik?□Daten und Formeln zur Berechnung der Arbeitslosenquote sowie deren Interpretation□Auswertung einer Stichprobe um Schätzwerte für die Grundgesamtheit zu gewinnen6Was besagt die „Nullhypothese“?□μ1 − μ2 = 0□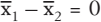

Die Lösungen finden Sie online unter www.uvk-lucius.de/brueckenkurse
1 Denn
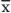
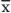
Текст предоставлен ООО «ЛитРес».
Прочитайте эту книгу целиком, купив полную легальную версию на ЛитРес.
Безопасно оплатить книгу можно банковской картой Visa, MasterCard, Maestro, со счета мобильного телефона, с платежного терминала, в салоне МТС или Связной, через PayPal, WebMoney, Яндекс.Деньги, QIWI Кошелек, бонусными картами или другим удобным Вам способом.




