Falacias, dilemas y paradojas, 2a ed.

- -
- 100%
- +
Ya hemos visto que la lógica trabaja con un lenguaje formal vaciado de contenido. Sin embargo, no es fácil poder determinar a simple vista la validez o corrección de un argumento. Para ello necesitaremos pruebas que nos conduzcan desde la verdad de las premisas a la verdad de la conclusión: (i) mediante la aplicación de las reglas de un cálculo lógico adecuado (derivación), es decir, que tenga la propiedad de ser consistente, de forma que en él no se puedan demostrar enunciados falsos, y completo, es decir, que demuestre todas las verdades o tenga la capacidad de fundamentar todo cálculo correcto; o, (ii) demostrando que no existe un contra-ejemplo, es decir, que no existe un caso en el que la premisa sea verdad y la conclusión falsa.
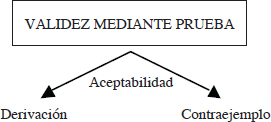
Cuando un argumento deductivo sea correcto, y además todas sus premisas sean verdaderas, tendremos entonces lo que en lógica simbólica se denomina argumento coherente. Un argumento coherente ha de tener necesariamente la conclusión verdadera, pues no puede darse el caso de que exista un argumento válido con premisas verdaderas y conclusión falsa. A este tipo de argumentos también se les denomina argumento coherente en la teoría de la argumentación. Por último, un argumento deductivo incorrecto o inválido puede ser un argumento formal falaz, o también, una falacia formal.
Diferencias en el ámbito de la teoría de la argumentación
Analicemos ahora algunas de las discrepancias que existen entre argumentación y argumento en el ámbito de la teoría de la argumentación.3 Una argumentación, o un argumento, es un encadenamiento de argumentos o de razones justificativas en apoyo de una afirmación o de una tesis, cuyo fin es convencer a alguien de su verdad. En otras palabras, se denomina argumento al conjunto de razones que se expresan y entrelazan con el ánimo de establecer algo, justificando una opinión o una acción, para que la persona ante quien se presenta el argumento o la argumentación acepte lo que se le presenta como conclusión o bien siga un determinado curso de acción.
La teoría de la argumentación parte de la validez formal de los argumentos, pues requiere la validez formal del argumento desde el plano de la lógica, de modo que de él se deduzca una inferencia lógica. A partir de aquí, se necesita que el argumento sea coherente desde el plano de la semántica, es decir, que contenga inferencia lógica y premisas verdaderas; y que sea cogente,4 es decir, que sea fuertemente convincente y, por lo tanto, que afecte a la psicología del receptor.
Por lo tanto, en la teoría de la argumentación el objetivo no consiste sólo en obtener una inferencia lógica que demuestre la validez del argumento, sino también en convencer o persuadir al oyente o al receptor de la verdad del argumento. Vemos pues que contiene tres elementos: (i) el sujeto: que es quien teje el argumento respetando las reglas de la inferencia lógica para producir un argumento válido en términos formales; (ii) el auditorio: que también aplica la lógica a aquello que recibe y que lo acepta como un argumento coherente; y, (iii) la psicología del receptor: que se deja seducir por la fuerza persuasiva del argumento coherente y lo capta como un argumento fuertemente convincente o argumento cogente.
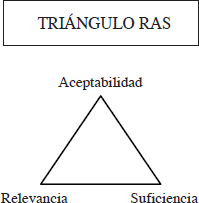
Lo anterior se encuentra enmarcado en el ámbito de la pragmática –del estudio de las significaciones de los signos para los sujetos– mediante la utilización del llamado triángulo RAS, que define las condiciones de relevancia, aceptabilidad y suficiencia que debe cumplir todo argumento genuino: (i) la razón de relevancia: según la cual deberemos rechazar aquellas razones que tengan poca o nula relación con la tesis que se pretende apoyar y justificar; (ii) la razón de suficiencia: por la que deberemos rechazar aquellos argumentos que tengan escasa capacidad para poder justificar y fundamentar la tesis; y, (iii) la razón de aceptabilidad: aunque la verdad sea siempre elusiva, esta tercera condición obliga a contrastar el contenido veritativo de la argumentación y, en la medida de lo posible, a verificar la veracidad de las premisas.
La lógica, la dialéctica, la retórica y la oratoria son disciplinas que se ocupan de la argumentación. Mientras que la lógica se encarga del análisis crítico de un texto o de un argumento, la dialéctica lo hace del procedimiento, en tanto que la retórica y la oratoria tienen por objeto embellecer las palabras mediante el estilo con el fin de persuadir al auditorio. Tanto es así que una falacia no existe simplemente porque alguien la elabore, sino que requiere que haya otros que incurran en ella para que podamos decir que existe como tal.
Lo usual es utilizar los términos falacia, sofisma o paralogismo en el mismo sentido, esto es, como un argumento aparente o forma de argumento o de refutación no válida con la que se quiere defender algo y confundir al contrario. A veces se distingue entre sofisma y falacia, entendiendo por falacia aquel argumento aparentemente válido que es simplemente un error o un descuido propuesto por alguien; mientras que por sofisma se entiende aquel argumento que ha sido tejido para hacer caer en él intencionadamente al auditorio o derrotar al oponente.
Otras veces se establecen algunas diferencias entre sofisma y paralogismo, entendiendo el sofisma como una refutación con conciencia de su falsedad y con el objetivo de confundir al contrario, de vencer mediante engaño; mientras que en el paralogismo falta dicha conciencia de falsedad, se trata de un pensar desviado y erróneo, pero involuntario y no intencionado. Además, el sofisma consiste en una refutación basada en pruebas no adecuadas, por lo que no es propiamente una refutación ya que es defectuosa.
Dentro de las falacias lógicas podemos distinguir de dos clases:5
a) falacias formales: son las que atentan contra una forma argumentativa válida, es decir, las que contienen una inferencia no fiable (i. e.: premisas verdaderas y conclusión falsa); como son la falacia de negar el antecedente y la falacia de afirmar el consecuente; y,
b) falacias no formales o materiales: que son las que nos interesan aquí, por tener mayor relevancia en el ámbito de la economía. Entre ellas podemos distinguir las siguientes:
1. Falacias informales del lenguaje: como las de ambigüedad (v. gr.: la falacia de composición, que es importante en economía y que consiste en afirmar del todo lo que es cierto de una parte sin mejor razón. Esta falacia nos ayuda a comprender la paradoja de la frugalidad, es decir, las razones por las que los intentos individuales de ahorrar en épocas de recesión, como la actual en España, pueden deprimir demasiado el consumo y llegar a disminuir los ahorros de todos) y las retóricas (v. gr.: Argumentum ad populum).
2. Falacias de relevancia o de apelación irrelevante: como la falacia de razón irrelevante (Non sequitur), la de conclusión irrelevante (Ignorantia elenchi), la de apelación a la persona o Argumentum ad hominem, la falacia de apelación a la autoridad o Argumentum ad verecundiam (v. gr.: Argumentum ad antiquitam), la de apelación a las emociones (v. gr.: Argumentum ad choleram, Argumentum ad baculum) y las falacias de distracción (v. gr.: Tu quoque).
3. Falacias de evidencia: como son las falacias de inferencia estadística (v. gr.: Secundum quid), las falacias de comparación, las de causa cuestionable (v. gr.: Post hoc ergo propter hoc que nos explica por qué algunos economistas confunden la forma en la que se manifiesta el crecimiento con los factores que lo determinan) y la de supuestos injustificados (v. gr.: Petitio principii, aunque ésta sea en realidad una falacia formal, y Argumentum ad ignorantiam).
4. Falacias adicionales: como las falacias de apelación a las consecuencias (v. gr.: Argumentum ad consequentiam).
En cuanto a los dilemas, señalemos que se trata de argumentos en forma de silogismo con una proposición disyuntiva cuyos dos miembros conducen a la misma conclusión; por eso se le llama syllogismus cornutus. En economía, solemos hablar de los dilemas en el mismo sentido que en el lenguaje corriente, es decir, como el conjunto de dos opciones contradictorias entre las que hay obligatoriamente que elegir una que producirá efectos negativos sobre la otra no elegida. En economía y en el marco de la teoría de juegos, es famoso el dilema del prisionero o, por poner un ejemplo más actual, el nuevo dilema que tiene planteado el Banco Central Europeo que consiste en la necesidad de gestionar una política monetaria que sea eficaz a la vez para países con inflación y para otros con peligro de deflación.
Por último, las paradojas consisten, como ocurre con las famosas aporías de Zenón de Elea, en proposiciones extraordinarias y abracadabrantes que, por una parte, aparecen como portadoras de verdad y, al mismo tiempo, van a contracorriente de la opinión convencional sobre un asunto. Se trata de argumentos que no cabe asimilar a un puro juego banal, más bien al contrario, constituyen un acicate para la revisión de los conceptos teóricos y de las doctrinas que desafían, pues como nos señala Giorgio Colli (2006: 22): «Las aporías suscitadas por Zenón no deben tomarse a la ligera, desde el momento en que grandísimos pensadores, como Aristóteles (...) y Kant, en la Crítica de la Razón Pura, intentaron superarlas». Tienen gran importancia en economía, como es el caso de la famosa paradoja de la frugalidad antes mencionada.
La argumentación y la ciencia
La pretensión de argumentar y de debatir, además de ser consustancial al hombre, es necesaria para poder vivir como tal. Hemos visto también que la argumentación es un juego de lenguaje en el que los participantes están comprometidos y se esfuerzan en conseguir, mediante el diálogo argumentativo, un acuerdo intersubjetivo y válido que añada conocimiento con pretensiones de verdad o de verosimilitud al ya existente. Es difícil, sin embargo, poder afirmar que un argumento cumple las pretensiones de validez cuando nos situamos en el marco de la racionalidad dialógico-trascendental (pragmático-universal) de Jürgen Habermas. La razón reside en que, según ésta, el diálogo intersubjetivo busca acuerdos con pretensiones de validez para los argumentos utilizados, y que dichos pactos están siempre sujetos a revisión y refutación ulterior. Es decir, estarán siempre aceptados con un carácter de provisión al modo en que Descartes, en la tercera parte de su Discurso del Método, decide elaborar «una moral para proveerse» (Quintás Alonso, 1999: 44) –une morale par provision– con el fin de no permanecer irresoluto en sus acciones.
La argumentación, por otro lado, es imprescindible para el avance de las ciencias, ya que toda ciencia de la que no se pueda demostrar que es falsa, falseada o falsada no puede ser ciencia. Como señala Thomas S. Kuhn (2006), las leyes científicas nunca se demuestran, pues aunque se confirmen en su validez al tener evidencia empírica a su favor, siguen siendo falseables. Si se llegase a demostrar la ciencia, entonces sólo tendríamos matemáticas y lógica simbólica, es decir, ciencias formales que enuncian verdades formales llenas de rigor analítico, pero vacías de contenido; mientras que las ciencias experimentales o empíricas, como la física o la química, enuncian verdades materiales que dan lugar a un corpus teórico del cual se obtienen leyes derivadas. A la física de Ptolomeo, que dicho sea de paso es la que utilizan los marineros por resultarles la más útil, siguió primero la de Copérnico y luego la desarrollada por Galileo. Esta última fue mejorada por Newton, y la de éste fue superada, a su vez, por la de Einstein.
Las leyes científicas empiezan siendo hipótesis, conjeturas, y no sabemos de dónde nacen dichas hipótesis; si surgen de las analogías, de la experiencia o de la intuición no lo sabemos con certeza. Aunque las falacias no son aceptables como argumentos genuinos, cumplen un importante papel en el avance de la ciencia en la medida en que ponen a prueba nuestros afanes por superar nuestros propios errores. Las ciencias empíricas, por ejemplo, se apoyan en razonamientos falaces debido a que no afirman mediante la utilización de reglas de derivación, como las matemáticas o la lógica, sino por empeiria, es decir, por una forma de conocimiento basado en la experiencia y en la observación, por oposición al conocimiento metafísico o especulativo.
En las ciencias no formales, las llamadas ciencias sociales, como la economía, el énfasis en la formalización matemática les añade rigor y las hace más útiles para el análisis y la predicción. Sin embargo, al mismo tiempo, el abuso de la matematización y la confianza ciega, y por otro lado no siempre justificada, en la formalización como palanca para hacerlas más científicas, las vacía de contenido, las aleja de la realidad económica que pretenden analizar y las vuelve rígidas, dogmáticas y, a veces, inservibles.
Es precisamente en los momentos de crisis, que en economía son recurrentes, cuando se manifiestan las «anomalías» (Kuhn), y es precisamente la existencia de «contraejemplos» lo que hace que se revisen acuerdos epistemológicos previamente pactados por la comunidad científica (paradigma científico). Por esta razón, es de esperar que surjan nuevos contraejemplos de la actual crisis financiera global que den lugar a revisiones epistemológicas de la ciencia económica en los próximos años.
Bibliografía
Alcolea Banegas, Jesús (2006): Curso sobre Teoría de la Argumentación, Universitat de València, Valencia, notas manuscritas.
Aristóteles (1988): Tratados de lógica [Órganon] ii. Sobre la interpretación, Analíticos Primeros, Analíticos Segundos, Biblioteca clásica Gre– dos, Madrid, vol. ii, 460 pp.
— (1988): Retórica, Gredos, Madrid, 626 pp.
Beneyto, Rafael y José Pedro Úbeda (2008): Lógica. Deducción natural, Departamento de Lógica y Filosofía de la ciencia, Universitat de València, curso 2008-2009 (mimeo), 147 pp.
Chalmers, Alan F. (2006): ¿Qué es esa cosa llamada ciencia?, Siglo XXI, Madrid, 247 pp.
Chalmers, Alan F. (2006): La ciencia y cómo se elabora, Siglo XXI, Madrid, 181 pp.
Colli, Giorgio (2006): Zenón de Elea. Lecciones 1964-1965, Sexto Piso, Madrid, 195 pp.
Copi, Irving M. y Carl Cohen (2007): Introducción a la lógica, Limusa, México, 698 pp.
Deaño, Alfredo (2007): Introducción a la lógica, Alianza, Madrid, 424 pp.
Falguera López, José Luís y concepción Martínez Vidal (1999): Lógica Clásica de Primer Orden: Estrategias de Deducción, Formalización y Evaluación Semántica, Trotta, Madrid, 482 pp.
Ferrater Mora, J. (2004): Diccionario de Filosofía, Ariel, Barcelona, vol. I, pp. 218-222 y 890-891; vol. ii, pp. 1208-1212, y vol. iii, pp. 2693-2700.
Garrido, Manuel (20054): Lógica Simbólica, Tecnos, Madrid, 540 pp.
Hempel, carl, G. (2006): Filosofía de la ciencia natural, Alianza, Madrid, 168 pp.
Kuhn, Thomas, S. (2006): La estructura de las revoluciones científicas, Fondo de Cultura Económica, México, 360 pp.
Miranda Alonso, Tomás (2002): Argumentos, Publicacions de la Universitat de València, Valencia, 105 pp.
Quintás Alonso, Guillermo (2002): Términos y usos del lenguaje filosófico, Publicacions de la Universitat de València, Valencia, 365 pp.
— (ed.) (2010): El discurso del método de Descartes, KRK Ediciones, Oviedo, 159 pp.
Tulmin, Stephen (2007): Los usos de la argumentación, Península, Barcelona, 330 pp.
Píldora 2
Trampas del lenguaje y economía6
A diferencia de lo que ha ocurrido con la lógica clásica de primer orden, con la psicología o con la filosofía analítica, las relaciones entre el lenguaje y la economía no han sido muy fecundas. A excepción de John Stuart Mill, la mayoría de los economistas no sienten una enorme inclinación hacia las sutilezas que encierran las paradojas lógicas o semánticas cuando se refieren al ámbito económico. Y ello es así a pesar de la enorme confusión que creamos los economistas cuando descuidamos nuestras expresiones semánticas y, al hacerlo, damos a entender a nuestro interlocutor una realidad muy diferente de la que queremos representar. Por eso, en lo que sigue, voy a intentar poner de manifiesto, con la ayuda de algunos ejemplos muy habituales, la importancia que tiene en economía saber distinguir con claridad los modos en los que una expresión lingüística puede ser significativa.
En efecto, habitualmente utilizamos expresiones del lenguaje natural que, mezcladas con argumentos de naturaleza económica o matemática, dan lugar a ciertos equívocos. E11o es debido, a veces, a las diferencias entre el significado de dicho lenguaje natural y su significado económico o matemático. Analicemos, por ejemplo, la frase «La renta per cápita de los españoles ha crecido dos veces más que la renta de los colombianos».
En ella estamos utilizando un sintagma diferencial con el que construimos una comparación en la que la expresión dos veces más tiene un significado doble:
a) Por una parte, podemos entender que dos veces más significa el doble de la cuantía inicial sobre la que establecemos la comparación, pues es esto lo que de una manera espontánea se nos viene a la mente. Según este significado, la frase querría decir que si los colombianos tienen una renta per cápita de digamos 100 euros, nosotros la tendríamos de 200 euros. En el lenguaje natural decir dos veces más tiene una representación psicológica que nos hace pensar en el doble, del mismo modo que cuando digo «tres veces más» o «diez veces más» estoy utilizando esta expresión como equivalente del «triple» o del «décuplo», y así me entienden los demás.
b) Sin embargo, si repasamos y repensamos la expresión dos veces más, nos daremos cuenta de que tiene otro significado, y que dicho significado no consiste en el doble. Decir el doble significa multiplicar por dos la dimensión del objeto que se esté considerando; mientras que, por el contrario, el doble sólo representa una vez más (¡y no dos veces!) aquello a lo que nos estamos refiriendo; sencillamente porque si fuese dos veces más tendríamos el triple y no el doble.
¿Cómo explicar toda esta confusión? Una primera aproximación al problema del significado de la expresión «dos veces más» la podríamos encontrar en Wittgenstein, para quien el significado de la palabra está determinado por su uso, es decir, «el significado es el uso que hacemos de la palabra» (2008: 137-141). En nuestro caso, el uso habitual que hacemos de la expresión «dos veces más», la figura mental que construimos es la del doble. Sin embargo, lo mismo ocurre cuando decimos «una vez más», pues la figura psicológica que se nos aparece es la de una extensión de igual tamaño a la que tenemos como muestra y que, por lo tanto, supone el doble del original.
En la lengua castellana, el sustantivo vez hace referencia a la operación matemática de multiplicar o de dividir dependiendo de lo que siga a continuación. Si lo que sigue es la voz más, entonces multiplicamos; si se trata de «dos veces más», multiplicamos por dos; si trata de «tres veces más», multiplicamos por tres. Pero, si lo que sigue es la voz menos, entonces dividimos, de modo que si se trata de «dos veces menos», dividimos por dos, o sea, estamos queriendo decir «la mitad», y si decimos «tres veces menos», dividimos por tres, es decir, estamos queriendo significar «un tercio».
Además de lo anterior, la voz más –como también sensu contrario la voz menos– hace referencia a la operación matemática de sumar, a la función aditiva de la suma. Por eso, cuando ambas funciones, la multiplicativa vez y la aditiva más, se confunden en una sola en la expresión lingüística dos veces más, objeto de nuestro análisis, en términos matemáticos estaremos multiplicando por dos, e inmediatamente después, añadiendo una unidad adicional al resultado de la anterior multiplicación, por lo que obtendremos el triple y no el doble.
Otro error de comprensión muy común entre los economistas, y que viene inducido por la falta de precisión en el uso del lenguaje, consiste en afirmar que el coste marginal de una producción cualquiera es el coste de la última unidad producida. Cuando en realidad el marginalismo razona, por el contrario, en términos de incrementos discretos y, por eso mismo, nunca habló de las unidades últimas, sino de las unidades adicionales o de una unidad más. Está claro que el coste de un determinado número de piezas es el mismo tanto para la primera pieza física que se haya producido como para la última, y que dicho coste se corresponde con el coste medio de producción o coste por unidad producida (coste unitario), es decir, con el coste total dividido por el número de unidades producidas.
Bibliografía
Blasco, Josep Lluís, Tobies Grimaltos y Dora Sánchez (2006): Signo y Pensamiento, Ariel Filosofía, Barcelona, 238 pp.
Garrido, Manuel (20054): Lógica Simbólica, Tecnos, 540 pp.
Wittgenstein, Ludwig (20084): Investigaciones Filosóficas, Crítica, Barcelona, 547 pp.
Píldora 3
Un poco de matemática, física y economía7
La economía ha venido promoviendo e impulsando una utilización muy intensa de las matemáticas con el fin, entre otros, de superar su complejo de inferioridad como ciencia. Sin que esto sea reprobable, pues es bueno que la economía se interese por el rigor y la forma, también sería bueno que a la par no se olvide del contenido, a menos que queramos convertirla en una disciplina más interesada en el rigor formal de sus métodos y modelos, y en la precisión de sus estimaciones y cálculos, pero completamente desvinculada de la realidad y desinteresada por la verdad de los argumentos económicos.
Además, la imposibilidad de llevar a la práctica verificaciones empíricas al modo de las ciencias experimentales ha inducido a la economía a utilizar las matemáticas muy intensamente. Como la economía no puede realizar experimentación, un recurso muy habitual ha consistido en utilizar la expresión caeteris paribus para poder verificar el impacto que produce el cambio en una variable cuando las demás se mantienen invariables. En términos matemáticos, esta expresión es equivalente al concepto de derivada parcial, y expresa la necesidad de establecer relaciones de causalidad sin ser entorpecidos por la interacción simultánea de los determinantes últimos de las variables económicas consideradas.
Otra expresión económica que puede dar lugar a cierto despiste conceptual es el término desaceleración económica, del que tanto se habló a principios del 2007. El Gobierno utilizaba esta expresión como eufemismo para negar la realidad y evitar la connotación negativa que tenían y tienen las palabras crisis o recesión. La obsesión por soslayar la cruda realidad y dulcificarla llevó al ministro de Economía y Hacienda a afirmar que la economía española se encontraba en una situación de desaceleración acelerada. Antes utilizar expresiones pintorescas y ejercitarse en el funambulismo lingüístico que reconocer abiertamente ante los españoles que estábamos ya al filo de la recesión.
En términos de la física y las matemáticas el concepto está muy claro, sobre todo cuando nos encontramos en el universo de las funciones. La física aplica las matemáticas para estudiar funciones concretas, como puede ser el estudio de la posición de un objeto o masa puntual. Por analogía con la física, podemos entender el crecimiento del PIB como la velocidad a la que se desplaza un objeto, que en el ámbito de la economía podría ser el PIB. En nuestro caso, la función que nos interesa es la derivada de la posición inicial con respecto al tiempo, que es la velocidad.










