Introducció a l'enginyeria dels reactors químics

2. Fenomenologia de les reaccions químiques

2.1 Introducció

Amb aquest capítol es pretén recordar una sèrie de conceptes, adquirits en altres àrees de la química i de l’enginyeria química, que conformen la base sobre la qual s’ha d’alçar el desenvolupament de l’enginyeria dels reactors químics. Així, en primer lloc, es recordaran algunes idees de l’estequiometria de les reaccions, per a representar els canvis de composició d’una forma condensada. A continuació, es revisaran molt breument alguns conceptes de l’equilibri químic i de la cinètica química. Amb tot això se situarà el mapa, i les característiques de l’espai, en què es desenvoluparan les reaccions. Finalment, es recordaran les expressions dels balanços de propietat en un sistema amb reaccions químiques, i s’adaptaran als reactors ideals.

2.2 Estequiometria

L’estequiometria estudia les proporcions en què reaccionen les espècies químiques. En l’estudi dels reactors químics aquestes relacions apareixen com a limitacions als canvis de composició que poden tenir lloc. També poden ser considerades des d’un altre punt de vista equivalent, ja que constitueixen l’aplicació de l’equació de conservació de la quantitat de cada espècie atòmica.

2.2.1 Esquema de reacció

Un esquema de reacció és l’equació que descriu la seua estequiometria, no necessàriament el seu mecanisme. La forma general de representar-la és

on S és el nombre d’espècies del sistema, Aj representa l’espècie j i vj és el seu coeficient estequiomètric. Si hi ha diverses reaccions la seua representació serà

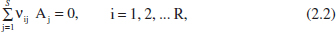
on R és el nombre de reaccions i vij és el coeficient estequiomètric de Fespècie Aj en l’esquema de reacció i.

Interessa treballar amb el menor nombre possible d’equacions, i per tant amb el menor nombre de reaccions. Hi ha procediments per a, coneguts els esquemes de reacció, determinar si hi ha entre ells alguna combinació lineal, per a eliminar-la i d’aquesta manera reduir la dimensió del problema. Així mateix, en la bibliografia hi ha altres procediments per a trobar un conjunt d’esquemes de reacció linealment independents, capagos d’explicar els canvis estequiomètrics que tenen lloc en el sistema. Aquesta opció és interessant en el cas que no es coneguen les reaccions que tenen lloc.

Exemple 2.1

El sistema format per les espècies N2, O2, NO i NO2, s’ha representat per dues reaccions:

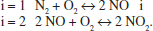
Podria haver-se representat només per una? Quants esquemes es necessitarien per a representar aquest sistema, considerant que hi ha, a més a més, dos òxids més: N2O i N2O4?

Solució:

Vegem, en primer lloc, el nombre d’esquemes de reacció necessaris per a representar aquest sistema. Per a això comencem fent un recompte:

Espècies: N2, O2, NO i NO2; és a dir, S = 4.

Elements: N, O; tenim, doncs, 2 elements.

Matriu elements-espècies: Els elements d’aquesta matriu assenyalen el nombre d’elements d’un determinat tipus que hi ha en una espècie determinada.

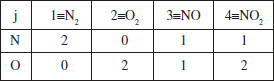
Es pot veure fàcilment que el rang d’aquesta matriu (l’ordre del determinant més gran no nul) és 2. És a dir, Rε = 2. Amb això, aplicant la regla de Gibbs, calculem R’, el nombre de reaccions independents necessàries per explicar el sistema. Regla de Gibbs: R’ = S - Rε = 2.

Per tant es necessiten dos esquemes. L’enunciat proposa dos esquemes també, que contenen les 4 espècies. Per a saber si són vàlids, cal fixar-se si són independents. Veiem que ho són, ja que cada esquema té almenys una espècie que no està en l’altre, per tant no es pot obtenir una relació a partir de l’altra. Es pot veure que si sumem totes dues reaccions desapareix l’espècie NO, per la qual cosa aquest esquema de reacció suma no pot explicar els canvis de composició en el sistema.

En aquest cas ha sigut fàcil comprovar la independència de les reaccions, a causa del seu reduït nombre. Per això, apliquem un procediment que es pot automatitzar i estendre a casos més complicats. En aquest procediment escrivim la matriu de coeficients, en la qual, fent operacions permeses, cal aconseguir que la «diagonal principal» estiga formada per «1» (serveix qualsevol número distint de 0), i la part situada davall d’aquesta «diagonal principal» per 0. Si s’aconsegueix açò, els esquemes de reacció són independents; en cas contrari, apareixerà alguna fila formada únicament per 0. Açò indica que aquest esquema de reacció és dependent d’altres esquemes del sistema, per la qual cosa ha de ser eliminat.

En el nostre cas la matriu de coeficients és

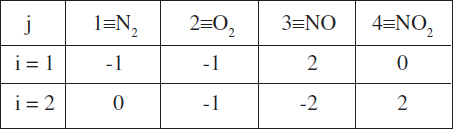
Es pot veure que, sense necessitat de fer cap càlcul, es té la situació buscada. Per això, els esquemes són independents.

Sobre el problema de la inclusió de dues espècies més (N2O i N2O4), podem veure que el nombre d’espècies serà ara S = 6. Aquestes dues espècies no afigen cap element nou (estan formades ambdues per N i O. Per això, Rε = 2, i R’ = 4). Es necessitaran, per tant, 4 esquemes de reacció.

Una altra possibilitat, en relació amb aquest problema, és que coneguem les espècies implicades (N2, O2, NO i NO2) i volem trobar uns esquemes de reacció que expliquen els canvis de composició del sistema. És a dir, suposem que l’enunciat no proposa cap esquema de reacció. Aleshores podem aplicar el mètode de Smith i Missen (1979, 1998). En aquest procediment, el punt de partida és la matriu elementsespècies descrita més amunt. Fent operacions elementals i raonables cal fer aparèixer la matriu identitat. La resta de la matriu ens donarà els coeficients estequiomètrics buscats. El problema plantejat és molt senzill, simplement cal dividir totes dues files per 2, i s’obté:

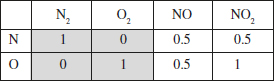
Les dues columnes que encapçalen la matriu identitat (marcada en gris) formen la base del sistema (N2 i O2). Les dues columnes que no pertanyen a la base ens donen els coeficients estequiomètrics de les formacions d’aquests components a partir dels de la base:

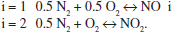
La solució no és única, per això aquestes reaccions no són les proposades abans (una si, l’altra no).

2.2.2 Mesura de la composició

La presència de reaccions en un sistema és percebuda pels canvis de composició que hi tenen lloc. Per això, en la taula 2.1 es recorden molt breument les formes més comunes de representar la composició.

TAULA 2.1

Variables de composició

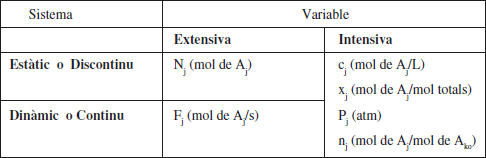
Ak és el component clau definit en l’apartat 2.2.3.1.

Les relacions entre aquestes variables són senzilles d’establir, per exemple:

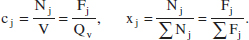
2.2.3 Mesures de l’avanç de la reacció

Aquestes variables indiquen els canvis de composició que tenen lloc en el sistema amb un sol valor per reacció. A continuació, es recorden algunes d’aquestes variables:

2.2.3.1 Grau de conversió

Representa la fracció reaccionada d’un component clau o de referència (Ak). Encara que l’elecció d’aquest component és bastant arbitrària, sol tractar-se d’un reactiu. En el cas que hi haja una sola reacció, es recomana l’elecció del reactiu limitador; quan coexistisquen diverses reaccions, sol triar-se un reactiu comú. Si no hi ha cap reactiu comú, pot utilitzar-se un component clau distint per a cada reacció, encara que en aquest cas es recomana utilitzar una altra mesura de l’avanç de la reacció. Si hi ha més d’un reactiu comú, les regles per a l’elecció del component clau es compliquen, per la qual cosa el més senzill és triar-ne un qualsevol, ja que, al cap i a la fi, es tracta d’un component a què referir els càlculs.

Així, per a sistemes en què hi ha una sola reacció (o si n’hi ha diverses, per a una d’elles),

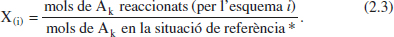
El parèntesi de Fequació (2.3) indica que si es té una única reacció no cal indicar-ho amb el subíndex. En cas contrari, quan hi ha diverses reaccions, cal indicar amb el subíndex la reacció de què es tracta. Alguns autors posen un subíndex, fent referènda al component clau, encara que no tinguen més que una reacció.

La situació de referènda * és:

- La inicial (a t = 0) per a un sistema discontinu.

- La de l’entrada del reactor per a un sistema continu.

Aquestes situacions de referènda s’il·lustren en la figura 2.1.

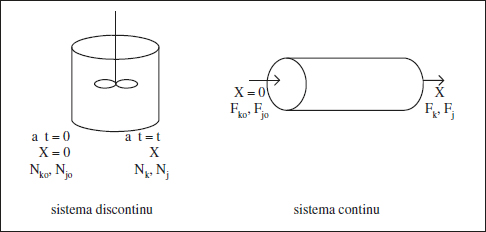
Figura 2.1. Situacions de referènda per a un sistema discontinu i un sistema continu.

Això porta a les següents equacions per als canvis de composició: - Si tenim una sola reacció, les variables extensives quedaran: Component clau:

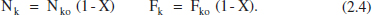
Per a qualsevol component:

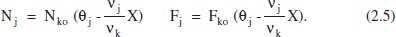
I el nombre total de mols del sistema:

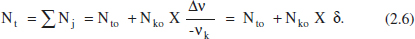
De la mateixa manera, el cabal molar total serà:

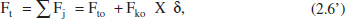
on

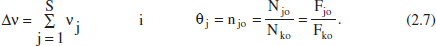
- I les variables intensives:

la rao molar nj:

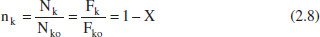
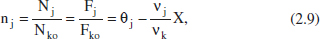
i la concentracio molar cj:

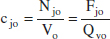
Aquesta variable mostra, tal com s’acaba de recordar, la relació entre el nombre de mols de l’espècie j i el volum del sistema. En avangar la reacció, poden canviar tots dos membres d’aquesta relació. Per això, es distingirà entre sistemes de densitat constant i aquells que són de densitat variable. En els sistemes de densitat constant, tenint en compte (2.4), (2.5) i (2.10), i que Vo = V (o Qvo = Qv ):

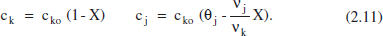
En els sistemes de densitat variable s’ha de descriure, a més a més, la variació de V(o de Qv) amb la conversió. Així, per exemple en un sistema discontinu gasós, el volum de reacció pot canviar, si l’entorn del sistema li ho permet, perquè canvia la pressió, la temperatura i/o el nombre de mols per la reacció química.

a temps t = 0 Po Vo = zo Nto R To en un altre temps t P V = z Nt R T

Dividint ambdues expressions i ordenant:

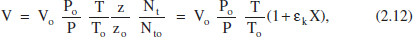
on s’ha considerat que el factor de compressibilitat (z) no canvia pràcticament. A més a més, l’ultim parèntesi representa la variació relativa del nombre total de mols a causa de la reacció, per al qual s’ha tingut en compte l’equació (2.6), i que anomenem εk al producte xko δ. Per a entendre el significat de εk, pot considerarse la seua definició alternativa, el canvi fraccional del volum de la mescla reactiva en completar-se la reacció a causa de la variació en el nombre de mols:

L’equació resultant per a cjen aquest cas és

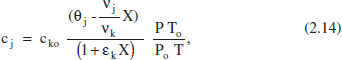
i per a la fracció molar xj,

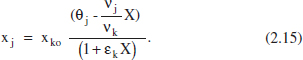
Si tenim diverses reaccions, les variables extensives quedaran: Component clau:

Per a qualsevol component:

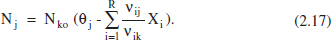
La traducció o extensió d’aquestes equacions a altres variables es pot efectuar seguint la metodologia exposada més amunt.

Exemple 2.2

Quina de les següents expressions correspon a la composició de B en un procés en què es desenvolupa la reacció en fase gas, elemental A + B → 2 C + D, en condicions no isotermes? L’aliment és equimolar en A i B.

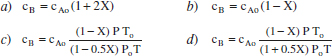
Solució:

Es tracta d’una reacció en fase gas: A + B → 2 C + D xAo = xBo = 0.5.

Com que Δv ≠ 0, el sistema pot ser de densitat variable. En aquest cas, Δv = -1-1+2+1 = 1, per la qual cosa, tenint en compte que s’ha triat A com a component clau,

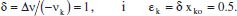
Per això, la solució serà la d. Si el sistema fóra un RDTA de V constant, el sistema seria de densitat també constant, amb la qual cosa la solució correcta seria la b.

2.2.3.2 Grau d’avang

La definició d’aquesta variable extensiva pot deduir-se de les següents expressions:

Només una reacció:

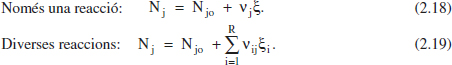
Cal adonar-se de les diferències entre el grau d’avanç (magnitud extensiva) i el de conversió (magnitud intensiva).

2.2.3.3 Rendiment

Hi ha moltes definicions per a aquest concepte, però una de les seues formes més simples seria:

Aquesta definició (rendiment global) s’ha de matisar afegint la relació estequiomètrica per a obtenir resultats raonables. Així,

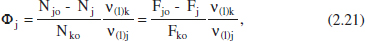
on (1) es refereix a l’esquema de reacció que condueix del component clau (Ak.) al producte d’interès (Aj). El rendiment puntual o instantani representa el quocient entre les velocitats de producció de Aj i de consum de Ak

2.2.3.4 Selectivitat

També en aquest cas es tenen moltes definicions per a aquest concepte, però una de les formes més simples seria

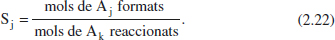
Aquesta definició també s’ha de matisar afegint la relació estequiomètrica per a obtenir resultats raonables. Així,

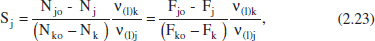
on (1) es refereix a l’esquema de reacció que condueix del component clau (Ak) al producte d’interès (Aj). Alguns autors anomenen selectivitat al que ací s’ha denominat rendiment puntual; per això, en cada cas caldrà establir la definició que s’està utilitzant. En el capítol 6 es tractaran aquests conceptes amb més amplitud.

2.3 Equilibri químic

En altres assignatures s’ha estudiat el càlcul de la composició en l’equilibri i la influència de diferents variables sobre aquesta composició. Ací simplement es vol recordar que l’equilibri químic marca un límit, és a dir, constitueix una restricció per a les variables que representen el sistema. Així, per exemple, la variable grau de conversió, tal com s’ha definit en l’apartat anterior, està acotada entre 0 i 1, però ara ho estarà entre 0 i Xe(grau de conversió en l’equilibri). D’aquesta manera, la zona permesa per a aquesta variable (i les composicions associades a ella) queda restringida a una regió menor que la que permeten els canvis estequiomètrics.

La conditió d’equilibri porta a un mínim de la funció de Gibbs, la qual cosa permet introduir el concepte de constant termodinàmica d’equilibri, per a cada una de les reactions:

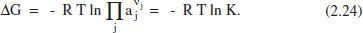
2.3.1 Influència de la temperatura

El punt de partida per a analitzar la influència de la temperatura sobre la composició en l’equilibri és l’equació de Van’t Hoff:

d’on es pot deduir que si la reacció és exotèrmica (ΔH<0), en augmentar la temperatura la constant d’equilibri A"disminueix, i amb ella també ho fa Xe. Al contrari, si la reacció és endotèrmica (ΔH>0), en augmentar la temperatura augmenta K,i amb ella Xe. Situations que estan d’acord amb el principi de Le Chatelier-Braun. La forma d’aquestes variations poden observar-se en les figures 2.9 i 2.10.

2.3.2 Altres influències

En diferents textos (Modell i Reid, 1974; Aris, 1969) es pot estudiar la influència de variables com ara pressió, presència d’inerts, composició initial, etc., i no s’analitzaran ací amb detail. No obstant això, es recordarà que aquestes variables no influeixen sobre K, però evidentment poden afectar la composició en l’equilibri.

2.4 Tipus de reactor

Tal com es va comentar en el capítol l hi ha una gran varietat de tipus, grandàries, formes, colors, etc. de reactors, per la qual cosa es procedeix a una classificació d’aquests:

2.4.1 Classificació dels reactors químics

2.4.1.1 Per la forma d’operar

Segons el tipus d’operació, els reactors poden ser discontinus, continus o semicontinus.

El reactor discontinu també es coneix com a intermitent, o per càrregues (batch), noms que descriuen el seu funcionament. El comportament d’aquest reactor és sempre no estacionari, funciona per cicles, és flexible i presenta un cost inicial baix. El producte pot presentar falta d’homogeneïtat entre les diferents càrregues (cicles).

El segon tipus és el continu. El comportament habitual d’aquest reactor és estacionari, resulta fàcil d’automatitzar i controlar, presenta menor cost d’operació, el producte sol ser molt homogeni.

El comportament semicontinu és intermedi (híbrid) entre els anteriors, per la qual cosa normalment serà no estacionari. La seua flexibilitat facilita el control de la temperatura. Presenta moltes disposicions. Per exemple, si tenim dos reactius, es pot introduir inicialment un dels reactius (discontinu) i després introduir l’altre de manera contínua. Una altra situació semicontínua correspon al cas en què un dels productes de la reacció és volàtil, el funcionament és bàsicament discontinu, excepte pel fet que aquell producte s’elimina contínuament. Aquest procediment pot facilitar la superació de les limitacions relacionades amb l’equilibri que apareixen en altres reactors. El comportament semicontinu proporciona una sèrie de graus de llibertat extra en les mans del dissenyador. En la figura 2.2 s’esquematitzen els funcionaments que s’acaben de comentar.

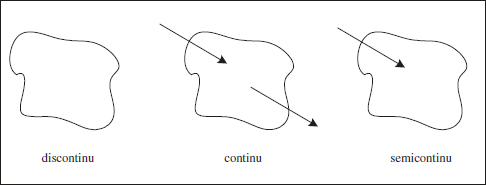
Figura 2.2. Esquemes dels reactors classificats per la forma d’operar.

2.4.1.2 Per la forma de circular o de posar en contacte la mescla reaccionant

D’acord amb la forma de circular la mescla reactiva, els reactors poden ser de tanc agitat o tubulars.

El nom de reactor tubular, a més de la referència a l’aspecte del reactor, indica que la mescla avança en una direcció i la composició canviarà en aquesta direcció, a causa de la reacció química (cj = f(z)).

En el funcionament conegut com de tanc agitat, l’agitació provoca una homogeneïtzació del sistema i no es troben variacions ni en la composició ni en la temperatura [cj ≠ f(x, y, z), T ≠ f(x, y, z)]. En la figura 2.3 s’esquematitzen els funcionaments que s’acaben de comentar:

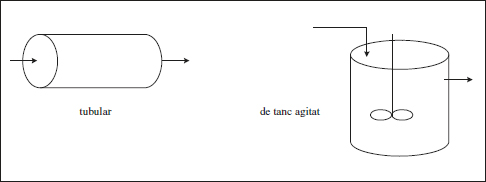
Figura 2.3. Esquemes dels reactors classificats per la forma de circular.

2.4.1.3 Per la forma d’intercanviar calor

D’acord amb aquest punt de vista un reactor pot ser:

Adiabàtic, quan no hi ha intercanvi de calor amb l’exterior (q = 0).

No adiabàtic, en cas contrari (q ≠ 0). Al seu torn, poden contemplar-se el comportament isoterm, en què l’intercanvi de calor és l’adequat perquè no hi haja canvi en la temperatura, i el no isoterm en cas contrari.

2.4.1.4 Per la naturalesa de les fases presents

Atenent la naturalesa de les fases presents, els reactors poden ser:

Homogenis, quan la mescla reactiva presenta una sola fase (gas o líquida).

Heterogenis, quan estan presents i intervenen en la reacció diverses fases (gas-líquid, gas-sòlid, líquid-sòlid, líquid-líquid, sòlid-sòlid, gas-líquid-sòlid, etc.). Per exemple, la polimerització per suspensió és una reacció homogènia, encara que hi haja diverses fases, perquè la reacció succeeix únicament en una d’elles (les gotes).

2.4.2 Reactors tipus o estàndard

A la vista de les classificacions anteriors, i per a facilitar l’estudi dels distints equips, es van proposar una sèrie de reactors ideals combinant distints aspectes d’aquelles. Els reactors ideals (comportament idealitzat) són:

– Reactor Discontinu de Tanc Agitat (RDTA).

– Reactor Continu de Tanc Agitat (RCTA).

– Reactor Continu Tubular o de Flux de Pistó (RCT o RFP).

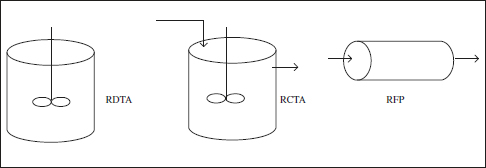
Figura 2.4. Reactors tipus, ideals o estàndard.