Introducció a l'enginyeria dels reactors químics

En els reactors de tanc agitat no hi ha cap problema a aplicar l’equació (2.37), ja que la concentració i la temperatura són uniformes. El reactor de flux de pistó no compleix aquesta conditió, per la qual cosa caldrà buscar un procediment alternatiu per a aquest reactor.

Vegem l’aplicació d’aquesta equació als diferents reactors de tanc agitat. Com que la concentració i la temperatura són uniformes, també ho serà la velocitat de reacció, per això la integral de (2.37) queda igual a Rj V, i

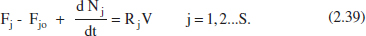
2.6.1.1 RDTA

En aquest reactor no hi ha entrada ni eixida, per la qual cosa Fj = Fjo = 0. L’equació (2.39) quedarà:

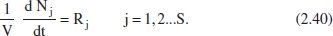
Si recordem la relació entre Nj i X(per manejar una sola equació). De (2.5) i (2.40):

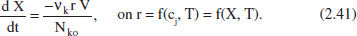
La transcripció gràfica d’aquesta equació es pot veure en la figura 2.12.

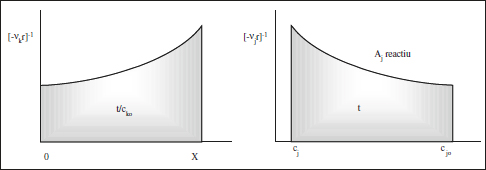
Figura 2.12. Transcripció gràfica de les equacions (2.41), (2.42), (2.58) i (2.59).

Aquest reactor és típic de reaccions en fase líquida (poden considerar-se freqüentment de densitat constant), però pot utilitzar-se amb sistemes gasosos (en estudis de laboratori, per exemple). Es poden tenir en compte dos tipus de reactor: a pressió constant i a volum constant. Si el sistema és de densitat constant no hi ha diferències entre ambdós comportaments, però en sistemes de densitat variable sí que hi ha diferències. Aquests aspectes són importants en les concentracions que apareixen en la velocitat de reacció, i, a més a més, si el volum és variable caldrà descriure aquesta variació. Aquestes diferències es manifesten en escriure l’equació (2.40) en funció de les concentracions:

Si el RDTA és de Vconstant,

La transcripció gràfica d’aquesta equació es pot veure també en la figura 2.12. S’ha de tenir en compte que cada una d’aquestes equacions conté una variable independent (una cj), però en r pot haver-n’hi d’altres. És a dir, aquestes equacions diferencials poden presentar un cert acoblament que obligue a resoldreles conjuntament. A poc que es complique el model cinètic es prefereix la solució numèrica.

Si es tracta d’un RDTA de V variable, l’equació (2.40) resulta:

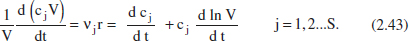
En el cas que hi haja diverses reaccions en el sistema, l’equació (2.40) quedarà:

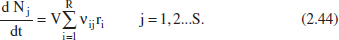
Per això, es disposa d’un sistema d’equacions diferencials que, probablement, caldrà resoldre de forma simultània.

2.6.1.2. Reactors continus

En analitzar els reactors de flux en estat estacionari desapareix la variable temps junt amb el terme d’acumulació. No obstant això, en el model apareix una altra variable amb unitats de temps. Aprofitem per definir aquesta variable i altres relacionades amb ella.

Temps espacial (τ): és el temps necessari per a introduir en el reactor un volum d’aliment igual al del reactor a les condicions de 1'aliment:

La velocitat espacial (S) és el nombre de volums d’aliment, iguals al del reactor a les condicions de 1'aliment, que poden introduir-se en el reactor per unitat de temps:

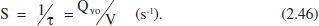
Temps mitjà de residència (θ): és el temps mitjà que roman en el reactor qualsevol porció macroscdpica de fluid. Així, per a un RCTA, tenint en compte que la conversió i les condicions en el reactor són uniformes, i que, per tant, el cabal que circula pel reactor és únic:

Per tant, si es tracta d’un sistema de densitat constant, el cabal volumètric no canvia des de l’entrada a l’eixida, i per això el temps espacial i el de residència coincideixen. En el cas contrari diferiran; així, si es tracta d’una reacció en fase gasosa en un RCTA, d’acord amb (2.12):

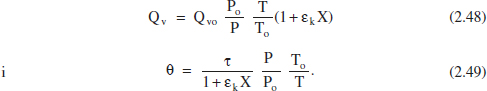
En un RFP, la mescla reactiva va avangant en direcció axial (z), i mentrestant va reaccionant i intercanviant calor. Aquests efectes (circulació, reacció i intercanvi de calor) poden afectar el valor puntual del cabal volumètric, és a dir, aquest cabal pot variar al llarg del reactor. A causa de la falta de constància del cabal volumètric dins d’aquest reactor, es fa necessari realitzar una anàlisi diferencial. Així, el temps de residència que li correspon a un element diferencial de volum serà:

Vegem un exemple per a aclarir aquests conceptes. Es disposa de dos reactors continus, un RCTA i un RFP, en ambdós casos es té el mateix cabal i a les mateixes condicions: Qvo = 4 m3/h, tots dos reactors són del mateix volum, V = 2 m3, la pressió i la temperatura no canvien des de l’entrada a l’eixida. Si, a més a més, en aquests reactors té lloc la reacció en fase gas A ↔ 3 B, 1'aliment està format només per A, i la conversió aconseguida en ambdós reactors és del 50 % (situació hipotètica realment estranya, plantejada únicament amb fins aclaridors), es tindrà ek = 2.

El cabal a l’eixida en ambdós reactors serà de 8 m3/h, per la qual cosa el valor del temps espacial i de la velocitat espacial seran comuns per als dos reactors: x τ 0.5 h i S = 2 h1. Per contra, el temps de residència serà distint en cada cas:

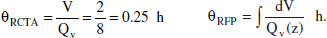
El temps espacial i el de residència són conceptes diferents, encara que 8 és més representatiu per a proporcionar una mesura més pròxima al temps que realment estan les porcions de fluid en el reactor i reaccionant, sol preferir-se τ per la seua facilitat d'tis.

• RCTA

En la figura 2.13 es mostra un esquema d’un RCTA. Si hi ha diversos corrents aliment, el corrent de l’esquema és la seua suma. Recuperem Fequació (2.39) i considerem una sola reacció. Encara que el comportament habitual serà estacio-nari, en aquest cas, per la seua senzillesa, s’analitzarà també el no estacionari.

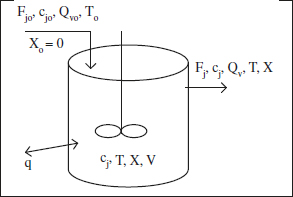
Figura 2.13. Esquema d’un RCTA.

- Comportament no estacionari (per exemple, posada en marxa).

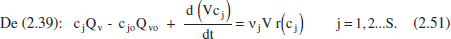
Si el sistema s’està omplint (O = 0) i a t = 0, V = V .

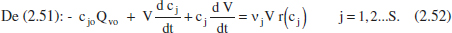
Del balang de matèria total en el sistema (admetent densitat constant) es té:

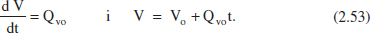
Les equacions (2.53) s’inclouran en les (2.52) per tal de tenir una única variable dependent en cada una d’elles (cj). El conjunt d’equacions diferencials (2.52) es pot resoldre numèricament o analíticament, però en tot cas es necessitarà conèixer les condicions inicials (en el reactor): a t = 0, cj = cjo (aquesta és la concentració inicial a 1'interior del reactor, no s’ha de confondre amb la de l’entrada).

Si el sistema s’ha omplit, i ix el mateix cabal que entra (Qv = Qvo , V = constant) i encara no s’ha assolit l’estat estacionari de (2.51):

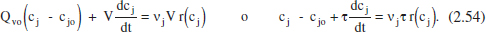
Una vegada assolit l’estat estacionari, l’equació (2.54) queda:

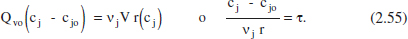
I en funció del grau de conversió, de per a j = k:

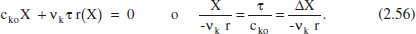
Les equacions anteriors es poden transcriure de forma gràfica (figura 2.14). La comparació d’aquesta figura amb la 2.12 mostra que, per a una situació «nor-mal» en què r es fa xicoteta en augmentar X, cal un temps espacial major en un RCTA que el corresponent temps de reacció en un RDTA per tal d’obtenir la mateixa conversió, tot mantenint iguals la resta de les condicions.

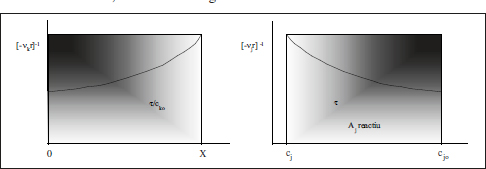
Figura 2.14. Transcripció gràfica de les equacions (2.55) i (2.56).

Exemple 2.8

Determineu la grandària del RCTA necessària per a portar a terme la reacció en els casos b i cde l’exemple 2.6. Raoneu el resultat.

Nota. La massa de catalitzador i el volum del reactor poden relacionar-se per l’equació Mcat = ρb V, en la qual ρb és la densitat global del llit catalític i val 500 kg/m3.

Solució:

En el cas de l’apartat bde l’exemple 2.6, la velocitat de reacció és negativa, la qual cosa indica que correspon a una situació fora del nostre abast, per tant, com que no es pot assolir, no té cap sentit físic. Per al cas c, aplicant l’equació dels gasos ideals, tenim cko = 0.002 mol/L, cTo = 0.02 mol/L, per la qual cosa Qvo = 2520 m3/h.

Del balanç de matèria en un RCTA, eq. (2.56) tenim:

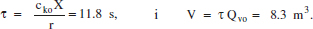
La velocitat de reacció és molt menuda, per la qual cosa el volum de reacció necessari és molt gran. Modificant les condicions d’operació es podria millorar considerablement el procés. Cal assenyalar que es tracta d’una reacció catalítica, i aquestes reaccions es duen a terme normalment en un reactor tipus RFP, i no en un RCTA.

• RFP o RCT

En la figura 2.15 es mostra un esquema d’un RFP. A més de l’aspecte de conducció i del funcionament continu (reactor continu tubular, RCT), aquest reactor ideal requereix que es complisca una hipòtesi: la circulació del fluid és francament turbulenta, a açò es refereix el nom de reactor de flux de pistó (RFP). El perfil de velocitat és pla, la qual cosa implica que totes les molècules tenen el mateix temps de residència en el reactor.

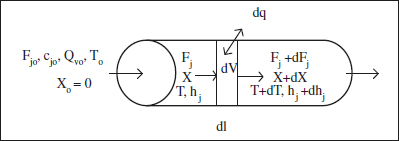
Figura 2.15. Esquema d’un RFP.

Com a conseqüència de la hipòtesi anterior, la composició canviarà únicament a la direcció axial. Atès que la composició varia d’uns punts a uns altres del sistema (la temperatura variarà o no d’acord amb el sistema d’intercanvi de calor), la velocitat de reacció també variarà. Per això, no serveix l’anàlisi macroscòpica realitzada en els anteriors reactors. Plantejant un balanç de matèria en el component j en l’element de volum dV, en estat estacionari, es té

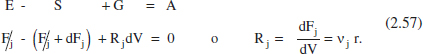
I si es tracta d’un sistema de densitat constant,

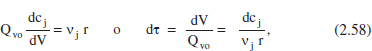
i en funció de X:

Les equacions anteriors es poden transcriure de forma gràfica tal com es pot veure en la figura 2.12, en aquest cas la variable temps, t, cal entendre-la com a temps espacial τ. La similitud entre les equacions del model del RDTA i del RFP és el resultat d’un funcionament semblant, encara que un discontinu i l’altre continu.

La forma no estacionària del balanc. de matèria en aquest reactor quedaria

D’aquesta manera s’han escrit les equacions del balanc. de matèria per als diferents reactors ideals. La utilització d’aquestes equacions estarà relacionada amb l’objectiu que es plantege. Així, en problemes de disseny, Fobjectiu és determinar les característiques del reactor (generalment el temps, que en els reactors continus es tradueix en el volum o en el cabal) que permeten obtenir una certa conversió o una producció determinada. En els problemes d’anàlisi s’estudia l’efecte d’alguna variable sobre el comportament del reactor.

2.6.2 Balang d’energia

Del mddul «Operacions Bàsiques de FEnginyeria Química» per al balanc. d’energia en sistemes amb reacció química (Aucejo i altres, 1999):

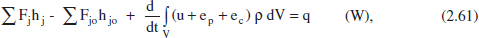
on s’han menyspreat les variations de Fenergia potential, Fenergia cinètica i la contribució del treball.

El terme q representa el flux de calor intercanviada, que es pot correspondre amb un valor donat (en el cas de calefactió elèctrica, per exemple), o en el cas que s’utilitze un fluid bescanviador pot venir donat per una equació com:

on T. és la temperatura del fluid bescanviador.

L’entalpia de l’espècie A en les condicions del corrent considerat es pot calcular amb l’equació (2.63), en el cas que no hi haja canvi de fase entre les dues temperatures considerades (la de referènda 298 K i la del corrent). En cas contrari, es modificarà adequadament aquesta equació:

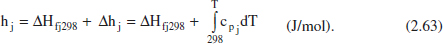
De nou resulta molt senzill aplicar l’equació (2.61) als reactors de tanc agitat, ja que la concentració i la temperatura són uniformes. No obstant això, aquesta aplicació requereix alguna simplificació, ja que en la mateixa equació s’utilitza energia interna i entalpia. Analitzant el terme d’acumulació, menyspreant de nou els termes d’energia potencial i cinètica enfront del de l’energia interna i aproximant aquesta per l’entalpia es té

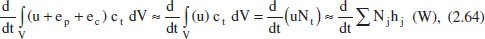
amb la qual cosa la (2.61) quedarà

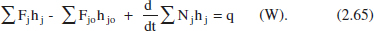
2.6.2.1 RCTA en estat estacionari

De la (2.65):

Escrivint aquesta equació en funció del grau de conversió per al cas en què hi haja una sola reacció:

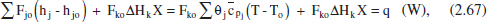
on s ha considerat que:

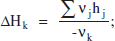
reordenant (2.67) i recordant (2.56):

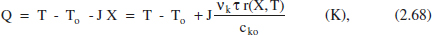
on

Si hi haguera diverses reaccions es tindria

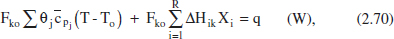
i

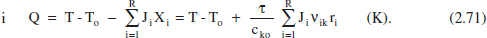
2.6.2.2 RCTA en estat no estacionari o RSCTA

L’equació (2.65) seria aplicable directament a un RCTA en estat no estacionari i a un RSCTA (reactor semicontinu de tanc agitat). Amb algunes transformations, es té:

2.6.2.3 RDTA

De F I’equació (2.65), i considerant que no hi ha entrada ni eixida, es té:

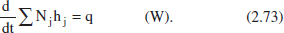
I desenvolupant aquesta equació com en el cas anterior:

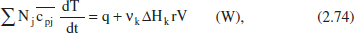
on es posa de manifest que l’evolució de la temperatura en el reactor es deu a les contributions dels efectes tèrmics de la reacció i de l’intercanvi. Desenvolupant aquesta equació en funció del grau de conversió, i considerant menyspreable la variació de la calor de reacció amb el temps (amb el canvi de temperatura associat), s’arriba a:

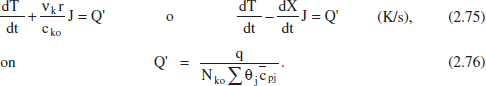
2.6.2.4 RFP o RCT

Si efectuem un balanc. d’energia en 1'element de volum dV (figura 2.15) en estat estacionari:

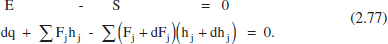
Desenvolupant el segon sumatori, simplificant i menyspreant els termes diferencials d’ordre superior, resulta:

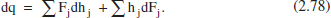
Reescrivint aquesta equació en funció del grau de conversió, per a sistemes en què només hi ha una sola reacció, i considerant menyspreable la variació de la calor de reacció amb la posició (amb el canvi de temperatura associat), s’arriba a:

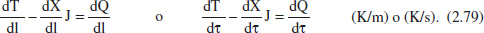
2.6.3 Balanç de quantitat de moviment

L’únic cas en què sol ser important aquest balang correspon al RFP (reactors tubulars), per ser utilitzat amb freqüencia per a reaccions en fase gas i estar constituït per conduccions de diàmetre xicotet. Atesa la influència de la pressió sobre la concentració, i d’aquesta sobre la velocitat de reacció, hauria d’incloure’s en el model.

Les equacions que permeten calcular la variació de la pressió al llarg del reactor són, entre altres:

– La de Haguen-Poiseuille, per a tubs buits i flux laminar (no és, per tant, un RFP):

on μ és la viscositat i <v> és la velocitat mitjana, ambdues del fluid. D és el diàmetre de la conducció (reactor).

– La de Fanning, per a tubs buits i flux turbulent:

on f és el factor de fricció i ρ la densitat del fluid.

– La d’Ergun, per a tubs amb farciment:

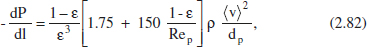
on ε és la porositat del llit i Rep és el mddul de Reynolds referit al diàmetre de la partícula (dp).

Qüestions, problemes i lectures d’ampliació

Qüestions

1. Quina de les següents expressions és 1'equació de disseny per a un RCTA? I quina ho és per a un RFP?

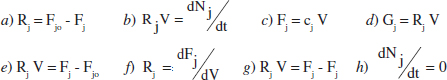
2. Una mescla de composició initial Njo reacciona fins a un grau d’avanç ξ, i una altra de composició initial N’jo ho fa fins a un grau d’avanç ξ, i llavors es mesclen. Demostreu que la composició que hi ha és la mateixa que si s’hagueren mesclat abans i reaccionaren fins a ξ £ ξ.

3. Seleccioneu la resposta més adequada per a les qüestions següents, raoneu molt breument l’elecció.

α) Quina suposició s’ha fet per a modelitzar un RFP ideal?

a) Que el reactor ix bé en la foto.

b) Estat estacionari i cap variació radial.

c) Sistema gasós i estat estacionari.

d) Flux laminar i sistema gasós.

β) Quina de les següents afirmacions no és una de les característiques dels RCTA?

a) S’usen generalment per a mescles liquides.

b) Mescla intensa.

c) La concentració a l’eixida és igual a l’existent en el reactor.

d) Gradient de concentració axial.

4. Quina de les següents expressions és l’equació de disseny per a un RDTA?

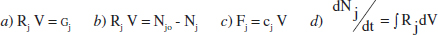
5. Estan tots els RTA perfectament mesclats?

a) Sí, els RTA són molt homogenis.

b) No, només els no ideals.

c) No, només els ideals.

d) No, només els que tracten sistemes líquids.

6. Assenyaleu de forma raonada entre les compositions següents les que no poden ser assolides. La reacció i la composició de partida es mostren en el problema 5. La temperatura d’operació és de 75 °C.

Problemes

1. La velocitat dels processos alimentaris no sol venir descrita en els termes convencionals de la cinètica química, probablement perquè el seu desenvolupament initial va correspondre a biòlegs o bioquímics i no a químics o enginyers químics. Així, una pràctica comuna en la indtistria alimentària consisteix a descriure la velocitat d’un procés en termes del paràmetre D, el temps de reducció decimal. Aquest concepte, per a una reacció del tipus Reactius → Productes, és el temps necessari perquè la concentració de reactius es reduïsca a la desena part del seu valor original. Trobeu la relació entre D i la constant cinètica k d’una reacció de primer ordre. La destrucció de microorganismes del tipus C. botulinum es pot representar d’aquesta forma, i per a aquesta reacció D val entre 0.1 i 0.3 min a la temperatura de referència (121 ºC), calcula els valors de k que li corresponen.

2. En la bibliografia sol trobar-se el valor de D121, és a dir, a 121 ºC (el concepte de D s’ha exposat en el problema 1, que és el valor típic de la temperatura en el procés d’envasament. La variació de D amb la temperatura també sol expressar-se en funció d’una variable distinta a l’energia d’activació. Es tracta del paràmetre z, el significat del qual és l’augment de la temperatura que redueix el temps necessari per a aconseguir una determinada conversió a la desena part. Trobeu la relació entre z i E. La destrucció de microorganismes del tipus C. botulinum presenta una energia d’activació de prop de 265-340 kJ/mol i un valor de z de 8-12 ºC; comproveu l’equació anterior amb aquestes dades.