Introducció a l'enginyeria dels reactors químics

- -
- 100%
- +
3. La dimerització 2 A (g) → A2 (g,l) es porta a terme en un RFP a 298 K i 2 atm (reactor isoterm). La concentració de A2 creix al llarg del reactor, i comença a condensar quan aconsegueix la saturació. Si s’alimenta A pur al reactor, per a quin valor de la conversió comença a condensar? Nota. Pot considerar-se que la pèrdua de pressió en el reactor és menyspreable. La pressió de vapor de A2 a 298 K és 0.5 atm.
4. Una mescla formada per SO2 (28 %) i aire (72 % en volum) s’introdueix contínuament en un reactor de flux (continu) en el qual es desenvolupa la reacció SO2 + 1/2 O2 ↔ SO3. Construïu una taula estequiomètrica en la qual es pose de manifest la influència del grau de conversió sobre els cabals molars i les concentracions de cada espècie. Finalment, representeu gràficament la variació de les concentracions amb X en el cas que la pressió total siga de 1485 kPa i la temperatura de 227 ºC. Comenteu els resultats. Dades i notes. Pot suposar-se comportament isoterm. Així mateix, es pot menysprear la caiguda de pressió del fluid en recórrer el reactor.
5. Es disposa dels següents valors de la conversió en l’equilibri per a la reacció elemental en fase aquosa A ↔ B, amb cAo= 1 mol/L i cBo= 0 mol/L.

6. Per a la mateixa reacció del problema 5 es coneix que la corba de r = 1 talla l’eix d’abscisses en T= 66.4 ºC i la de r = 3 en T= 90 ºC. Quant valen l’energia d’activació i el factor preexponencial per a la reacció directa? Quant val l’energia d’activació de la reacció inversa? Si, a més a més, es considera que el punt (X = 0.14, T = 70 ºC) pertany a la corba de r =1, quant val el factor preexponencial de la reacció inversa?
Nota. r ve donada en mol/L s.
7. La reacció irreversible en fase gas catalitzada per un sòlid A + B → C + D es porta a terme de manera isotèrmica en un reactor diferencial que conté el sòlid com a rebliment. S’han obtingut els resultats que es mostren en la taula P2.7.
TAULA P2.7
Informació cinètica de la reacció A + B → C + D
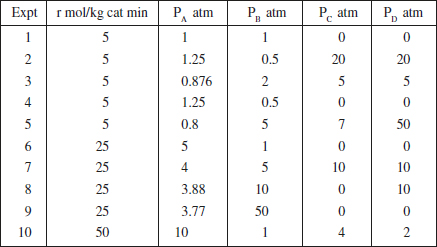
a) Quins experiments triaríeu per a determinar la influència de C i D sobre r? Quina és aquesta influència?
b) Quins experiments triaríeu per a determinar la influència de A sobre r? Quina és aquesta influència?
c) Coneguda la influència de A, C i D sobre r, què opineu sobre la influència de B? Creieu que és més complexa?
8. Considerem que la reacció irreversible en fase gas 2 A → B + C +3 D és de segon ordre en A. La mescla reaccionant inicial està formada per un 50 % de A i un 50 % d’inert. Si la reacció es desenvolupa mantenint constant la pressió i la temperatura, deduïu una expressió que mostre la variació del volum amb la conversió de A. Escriviu el model cinètic en funció també de la conversió.
9. Es disposa de la següent informació sobre la reacció en fase aquosa A1 ↔ A2. Coeficients cinètics: k = 3 107 exp (-11600/RT) s-1, k’ = 1.6 1018 exp (-29600/RT) s-1. Calor de reacció = -18000 cal/mol.
a) Determineu la relació entre la constant d’equilibri Kc amb la temperatura.
b) Assenyaleu alguna raó per a suposar que el sistema es comportarà de forma ideal des del punt de vista termodinàmic.
c) Construïu el diagrama d’equilibri (taula i gràfica conversió temperatura), considerant que la composició de referència és: Concentració de A1 = 1 mol/L, i Concentració de A2 = 0.5 mol/L.
d) Calculeu i dibuixeu diverses línies de r constant en el diagrama anterior, mantenint les mateixes composicions de referència.
Lectures d’ampliació
AUCEJO A. i altres (1999): Introducció a l’Enginyeria Química, Barcelona, Enciclopèdia Catalana.
CHEN, N. H. i R. ARIS (1992): «Determination of Arrhenius constants by linear and nonlinear fitting», AIChE Journal, 38 (4), pp. 626-628.
CUSACK, R. W. (1999a): «A fresh look at reaction engineering», Chemical Engineering, 106 (11), pp. 134-146.
—(1999b): «Reaction engineering. Part 2. Choosing the right reactor», Chemical Engineering, 106 (13), pp. 80-85.
DREAM, R. F. (1999): «Heat transfer in jacketed vessels», Chemical Engineering106 (1), pp. 90-96.
FONTIJN, A. i W. FEIDER (1977): «HTFFR kinetics studies of Al + CO2 → AlO + CO from 300 to 1900 K, a non-Arrhenius reaction», Journal of Chemical Physics, 67 (4), pp. 1561-1569.
MODELL, M. i R. C. REID (1974): Thermodynamics and its applications, Englewood Cliffs, New Jersey, Prentice Hall.
SMITH, W. R. i R. W. MISSEN (1979): «What is chemical stoichiometry?», Chemical Engineering Education, 13 (1) pp. 26-32. Una versió més actualitzada es pot trobar en: Chemical reaction stoichiometry (CRS) tutorial, Java applet, and resources, http://chemengineer.about.com/science/chemengineer/gi/dynamic/offsite.htm? site=http%3A%2F%2Fwww.chemical-stoichiometry.net%2Ftutorial.htm.
STEVE, E. H. (1997a): «More reactor design considerations. Part 2», Chemical Engineering, 104 (12), pp. 100-102.
—(1997b): «Reactor design considerations. Part 1», Chemical Engineering, 104 (12), pp. 96-99.
—(1998a): «Aspect ratio and jacket zoning in reactor scale-up. Part 4», Chemical Engineering, 105 (1), pp. 96-98.
—(1998b): «Jacket zoning in reactor scale-up. Part 3», Chemical Engineering,105 (1), pp. 92-95.
3. Reactors ideals. Comportament isoterm
3.1 Introducció
En el capítol anterior s’han estudiat els conceptes bàsics per a poder abordar l’anàlisi i el disseny d’un reactor ideal. Aquest model estarà format, principalment, pels balanços de matèria i energia, així com per les equacions de velocitat i les restriccions.
Les equacions dels balanços són equacions algebraiques o diferencials, en les quals participen (en ambdues) la composició (X en el cas més simplificat) i la temperatura.
Aquest model pot utilitzar-se per a predir el comportament del reactor, és a dir, per a contestar preguntes del tipus: què succeiria si…? Per exemple, què succeiria si fixàrem determinades condicions d’operació?, i si modificàrem algunes d’aquestes condicions? En aquest cas s’hauran de resoldre les equacions del model de manera simultània, ja que les variables implicades en la resposta del sistema (per exemple, X i T) apareixen en ambdues equacions. En algunes ocasions es poden resoldre les equacions dels balanços de forma separada, la qual cosa sol simplificar el problema. El comportament isoterm és un d’aquests casos simplificats, ja que una de les variables (T) deixa de ser-ho. Si aquest paràmetre és conegut, es pot utilitzar el balanç de matèria per a determinar la conversió aconseguida en el reactor, o el volum necessari per a assolir un grau de conversió establit, i el d’energia per a determinar el flux de calor que cal intercanviar.
En el capítol anterior s’ha mostrat alguna aplicació del balanç de matèria al càlcul del volum de reactor (o del temps de reacció) necessaris per a aconseguir una determinada conversió, o viceversa (exemple 2.8). Ací s’insistirà en els aspectes energètics i d’optimació. L’objectiu d’aquest capítol és mostrar l’aplicació dels balanços al disseny dels reactors ideals, així com a l’anàlisi del seu comportament, ambdues operacions en el comportament isoterm. Finalment, ens demanarem per aquelles situacions en les quals aquest comportament és el més interessant.
3.2 RCTA
Aquest reactor, tal com s’ha assenyalat en el capítol anterior (apartat 2.4.2), consisteix en un recipient ben agitat amb un funcionament continu. Una perfecta agitació és fonamental en aquest reactor. El disseny de l’agitador cau fora de l’objectiu d’aquest llibre. Rase (1977) en parla en la seua obra; així mateix, es pot recomanar el treball de Dickey (1991).
Les equacions del model en aquest cas són equacions algebraiques. A continuació es completarà el model, format pel balanç de matèria, amb els aspectes energètics, i es faran algunes aplicacions. El comportament isoterm implica que T = To.
3.2.1 Sistemes d’intercanvi de calor. Modelització
Els sistemes d’intercanvi per a aquest reactor poden ser: camisa (el reactor té una doble paret, deixant un espai per on circula el fluid bescanviador), serpentí (intern o extern) i bescanviador de calor extern. També pot utilitzar-se calefacció d’origen elèctric mitjançant una resistència submergida o una manta calefactora que li donarà calor a través de la paret. Aquesta opció elèctrica és costosa, motiu pel qual si s’utilitza serà en reactors de grandària reduïda. En la figura 3.1 es mostra un esquema d’alguns d’aquests sistemes:
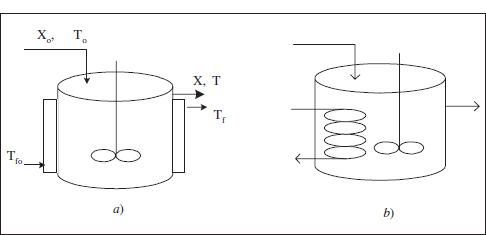
Figura 3.1. Sistemes d’intercanvi en un RCTA. a) Bescanviador de doble paret. b) Serpentí intern. Tf és la temperatura del fluid bescanviador, el subíndex o fa referència a les condicions d’entrada.
3.2.1.1 Bescanviador de doble paret (camisa)
Si considerem que en aquest cas s’utilitza un fluid bescanviador que canvia de fase, de manera que Tfo = Tf, podem escriure
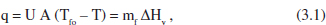
on mf és el cabal de fluid bescanviador que canvia de fase i AHv l’entalpia de canvi de fase. Substituint q en la definició de Q donada en l’equació (2.69):
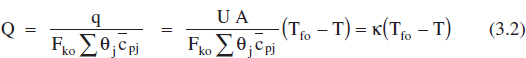
Pot demostrar-se (Aris, 1973; Escardino, 1996) que els altres sistemes d’intercanvi de calor poden representar-se per equacions com la (3.2), encara que les definicions de K(constant que caracteritza l’intercanvi de calor) varien evidentment d’uns casos a altres. De tota manera, es pot afirmar que K creix en fer-ho els termes UA i mf cpf, i en decrèixer Fko Σθjcpj.
3.2.2 Relació X-τ(Qvo, V) per a distintes cinètiques
A tall d’exemple es mostrarà Faplicació del model del balanc. de matèria a una cinètica d’ordre zero. Suposem que es tracta d’un sistema de densitat constant. Reacció: A → productes… r = k.
Aplicant el balanc. de matèria a un RCTA, equacions (2.55) i (2.56),
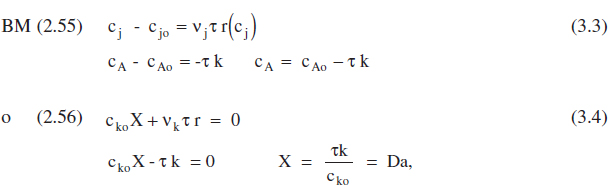
on Da és el mòdul de Damköhler per a una reacció d’ordre zero. Aquestes equacions es mostren gràficament en la figura 3.2.
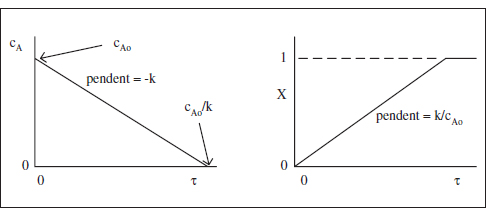
Figura 3.2. Variació de la concentració del reactiu i de la conversió amb el temps espacial, τ, en un RCTA per a una reacció d’ordre zero (ρ constant).
D’altra banda, si es tractara d’un sistema de densitat variable, prenent l’equació (2.39) en estat estacionari com a punt de partida:
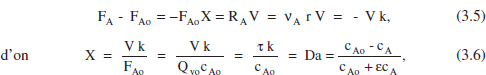
que donarà la relació cA-τ. Veiem que la relació τ-X és la mateixa en tots dos casos, és independent, doncs, per a aquesta cinètica, de si la densitat és constant o no. No és el cas de la relació cA- τ. En el capítol 4 de l’Omnibook de Levenspiel (1993) es poden consultar les aplicacions d’aquests balangos a altres cinètiques. En la taula 3.1 es poden veure algunes de les equacions resultants.
TAULA 3.1 Mòdul de Damköhler (Da) i relació X-Da per als distints reactors ideals i diferents cinètiques de la reacció A → productes

Exemple 3.1
En un RCTA en estat estacionari té Hoc, en fase líquida i de manera isoterma, una reacció elemental de dimerització 2 A → B. Es requereix una equació que permeta obtenir la conversió assolida en el reactor en funció del temps espacial. Compareu aquesta equació amb la mostrada en la taula 3.1, i justifiqueu les diferències.
Solució:
El balan§ de matèria en un RCTA queda Cj - Cj0 = Vjτr(Cj), i per a la cinètica esmentada:
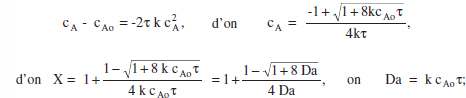
les diferències es deuen a l’estequiometria.
3.2.3 Flux de calor intercanviat
El flux de calor necessari per a mantenir T = T durant el procés es determinarà del balang d’energia, equació (2.68):
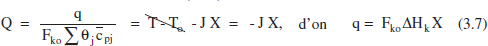
Cal insistir que el terme —J X del balanç d’energia no representa la generació d’energia (l’energia és una magnitud conservada). El flux de calor q haurà de ser proporcionat pel sistema d’intercanvi. Adonem-nos que si es tracta d’una reacció endotèrmica (ΔH > 0), q > 0, lògicament per a desenvolupar-la de forma isoterma s’haurà d’aportar un flux de calor determinat. Si es tracta d’una reacció exotèrmica (ΔH
3.2.4 Producció
En aquest cas, la producció serà el cabal de producte (P) que s’obté del reactor, d’acord amb l’equació (2.39):

on es pot veure que per a una gran producció es necessita disposar d’un volum de reacció elevat i/o d’una elevada velocitat de reacció.
Exemple 3.2
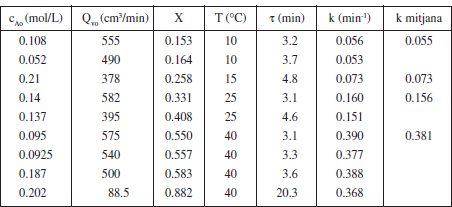
La hidròlisi de solucions aquoses dilu'ides d’anhídrid acètic té Hoc d’acord amb l’esquema (CH3CO)2O(1) + H2O(1) → 2 CH3COOH (1). La reacció és irreversible i de segon ordre (de primer ordre parcial respecte de cada un dels reactius). Tanmateix, com que 1' aigua actua com a dissolvent també i està en gran excés, podem considerar-la únicament de primer ordre respecte de l’anhídrid. La cinètica de la reacció s’ha estudiat en un RCTA de 1.8 L de volum que funciona de forma isoterma. Els resultats d’una sèrie d’experiments es mostren a la primera part (primeres quatre columnes) de la taula E3.2. Comproveu que la reacció està ben representada per la cinètica proposada, calculeu la constant de velocitat de reacció a cada temperatura i l’energia d’activació d’aquesta.
TAULA E3.2 Resultats d’una anàlisi cinètica de la hidròlisi de solucions aquoses diluïdes d’anhídrid acètic. Les quatre primeres columnes de la taula són els valors experimentals, les altres dues columnes són valors calculats a partir dels anteriors. L’última columna de la taula conté les mitjanes de k per a cada temperatura
Solució:
Com que de cada experiment tenim una velocitat de reacció, es tractarà d’avaluar el coeficient cinètic per a cadascun d’ells. Comprovarem que és de primer ordre observant que aquell coeficient pren pràcticament el mateix valor per a cada temperatura. Així mateix, si els valors de k varien amb la temperatura d’acord amb 1' equació d’Arrhenius, n’estarem més segurs.
La reacció és (CH3CO)2O(1) + H2O(1) → 2CH3COOH(1), és a dir, -A1, - A2, + 2 A3 = 0.
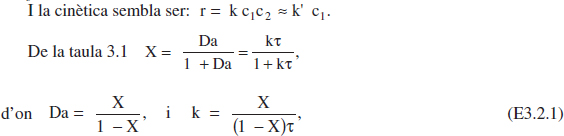
d’aquesta manera, per a cada valor de Qvo (o el que és el mateix, de τ) hem calculat el valor de k. Es pot veure que els valors de k són pràcticament coincidents per a cada temperatura, en la taula E3.2 es mostren els valors mitjans. Aquests valors segueixen el model d’Arrhenius, els paràmetres d’aquest model són: A = 4.68 107 min"1, i E = 11579 cal/mol.
Exemple 3.3
La descomposició irreversible de A1 s’efectua en presència d’una altra espècie qufmica A2 que actua com a catalitzador (romanent constant la seua concentració al llarg de la reacció). Experimentalment, s’ha trobat la segtient equació de velocitat per a la citada reacció: r = 1.30 c1 c201/2, on r ve expressada en mol/L min, i c1, i c20 en mol/L.
En un RCTA, de 10 m3, es vol descompondre A1 en dissolució, en presència del catalitzador mencionat, que es trobarà present amb una concentració de 0.002 mol/L.
a) Si es vol que el corrent que s’extrau del reactor, quan funciona en règim estacionari, no continga més del 5 % de la quantitat del component A present en el corrent aliment, quin cabal volumètric s’ha d’introduir al reactor?
b) Si en la posada en marxa del reactor aquest s’ompli ràpidament fins al seu volum total amb la dissolució aliment, continuant introduint aquest amb el cabal calculat en l’apartat anterior, quant de temps haurà de transcórrer fins que la concentració de A en el corrent que s’extrau del reactor continga un percentatge de A, igual al 6% del que està present en 1'aliment?
Solució:
El model cinètic per aquesta reacció és r = 1.30c1C2o1/2 = 5.810-2 c1, (mol/L min) és doncs el d’una reacció de pseudoprimer ordre.
a) El grau de conversió és del 95 %. El balanç de matèria queda
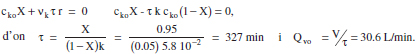
b) Posar en marxa el reactor. Temps necessari per tal que X = 0.94. Cal analitzar el problema considerant règim no estacionari (si el sistema s’ha omplit i sobre'ix el mateix cabal que entra, és a dir, Qv = Qvo, V = constant):
De (2.54):
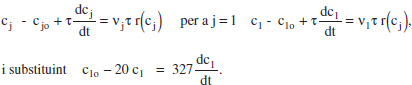
Amb les condicions inicials (en el reactor): a t = 0, cj = c’jo. En aquest cas, c1 = c’lo = clo.
La solució de l’equació diferencial és c1 = clo[0.05 + 0.95exp(-0.061 t)], d’on el temps necessari perquè c1 = 0.06 clo, és 74.4 min. El temps per a assolir una conversió del 95 % seria infinit.
3.3 RDTA
3.3.1 Sistemes d’intercanvi de calor
L’aspecte d’aquest reactor és molt semblant al del RCTA, però es diferencia en 1’absèntia de corrents d’entrada i eixida, i en el fet que el seu comportament és sempre en estat no estacionari. Aquestes condicions canviants amb el temps faran que el flux de calor intercanviat per a mantenir constant la temperatura haurà d’evolucionar també amb el temps. Tot això fa que aquest comportament siga fàcil de calcular, però més difícil de portar a la pràctica. Aquesta dificultat rau en el fet d’haver de dosificar el flux de calor intercanviat al llarg del procés (q). Aquesta dosificació s’aconseguirà modificant algunes de les variables que afecten q (el cabal i la temperatura del fluid bescanviador, Farea d’intercanvi, etc.).
Aquestes afirmacions poden xocar un poc amb la nostra experiència quotidiana al laboratori, en el qual s’utilitzen freqüentment aquests reactors de forma isoterma, la qual cosa s’obté introduint el reactor en un bany amb regulació de temperatura. Cal tenir en compte que en aquests aparells s’està malgastant un flux d’energia cap a l’ambient, que no seria permissible a una escala superior.
3.3.2 Relació X-t, per a distintes cinètiques
A tall d’exemple es mostrarà l’aplicació del model del balanc. de matèria a una cinètica de primer ordre. Suposem que es tracta d’un sistema de densitat constant.
Reacció: A → productes, r = k cA.
Aplicant el balanç de matèria, equació (2.42):
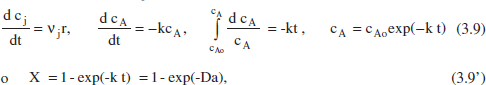
on és fàcil adonar-se que el grau de conversió, per a aquesta cinètica, és independent de la concentració inicial. La representació d’aquesta equació es pot veure en la figura 3.3. En la taula 3.1 es poden veure algunes de les equacions resultants per a diferents cinètiques.
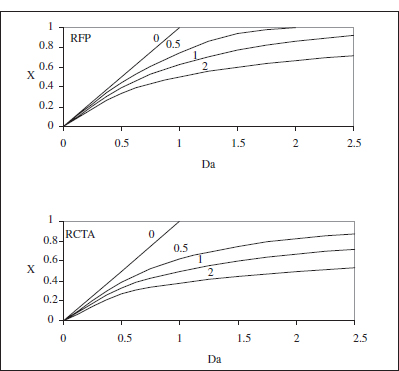
Figura 3.3. Variació de la conversió amb el temps espacial (Da) en un RFP (RDTA) i en un RCTA per a una reacció irreversible. El paràmetre indica l’ordre de la reacció.
D’altra banda, si es tractara d’un sistema de densitat variable, prenent F equació (2.43) com a punt de partida:
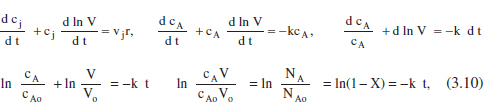
que donarà la relació cA-t. En aquest cas, la relació X-t, que es dedueix de F equació (3.10), és la mateixa que en el sistema de densitat constant. En el capítal 2 de F Omnibook de Levenspiel (1993) es poden consultar les aplicacions d’aquests balangos a altres cinètiques.
3.3.3 Flux de calor intercanviat
Per a calcular el flux de calor [q = f(t)] necessari per tal de mantenir el comportament isoterm s’utilitzarà el balang d’energia [equacions (2.75 i 2.76)] combinat amb el de matèria [equació (2.41)]:
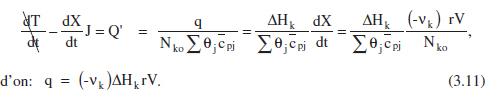
El flux de calor intercanviat és, doncs, proportional a la calor de reacció, al volum del sistema i a la velocitat de reacció. Com que la velocitat de reacció variant amb la composició (excepte si la reacció és d’ordre zero), i aquesta ho fa amb el temps, q s’haurà d’adaptar a aquesta evolució.
Si q és d’origen elèctric s’haurà de regular per a aquesta variació. Si s’utilitza un fluid bescanviador, q = U A (Tf-T), l’evolució desitiada es pot obtenir, per exemple, modificant Tf(t). Així, de l’equació (3.11):
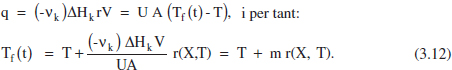
L’equació (3.12) mostra que Tf haurà de variar linealment amb la velocitat de reacció, r. Si la reacci6és endotèrmica (ΔH > 0), m > 0, Tf > T (es tractarà d’un fluid calefactor), en transcórrer la reacció (i el temps), X creix i r normalment disminuirà, amb la qual cosa Tf també ho farà. És a dir, les necessitats d’aportació calorífica van disminuint, i per això el fluid calefactor ho és cada vegada menys. Si la reacció és exotèrmica (ΔH










