Introducció a l'enginyeria dels reactors químics

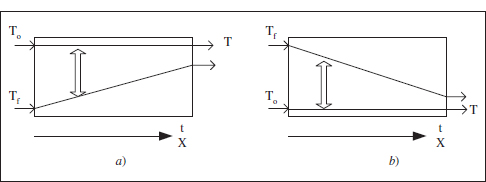
Figura 3.4. Evolució de Tf durant l’operació d’un RDTA. a) Reacció exotèrmica, b) Reacció endotèrmica.

En el cas d’una reacció endotèrmica, aquesta regulació es pot aconseguir actuant sobre la vàlvula que controla la pressió del vapor de calefacció; obrint progressivament aquesta vàlvula, disminuirà la pressió, i amb ella la temperatura de condensació.

Suposem, doncs, que es tracta d’una reacció endotèrmica i que es disposa de vapor de calefacció, la temperatura del qual es pot variar, tal com s’acaba d’exposar, entre Tf* i Tf*. Aquests límits vénen fixats per les limitacions de l’equipament de que es disposa. Com que al llarg del procés Tf* ha de disminuir (figura 3.4b), pareix raonable començar en el valor màxim, Tf*. Aquesta decisió permet determinar l’àrea d’intercanvi de calor necessària, aplicant l’equació (3.12) a Finstant inicial:

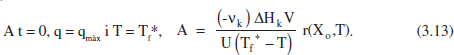
Amb aquest valor de A es pot determinar la variació de Tf durant la reacció. En el cas que Tf assolisca el valor mínim abans d’arribar a la conversió desitjada, es pot bloquejar una part del sistema d’intercanvi modificant simultàniament Tf. Els reactors grans poden tenir diferents zones d’intercanvi de calor per tal de poder adaptar-se a diferents situacions, per exemple diferents valors del flux de calor necessari o diferents volums de reacció. Si es decideix elevar de nou Tf al seu valor màxim es tindrà

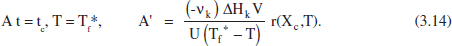
El temps en què té Hoc el bloqueig d’una part de l'area d’intercanvi és tc. L’àrea bloquejada serà ΔA = A - A’, i l’evolució de Tf vindrà donada per 1’equació (3.12) amb el valor adequat de l'area (figura 3.5). És a dir,

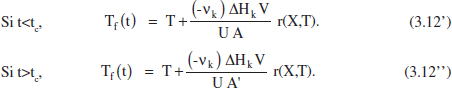
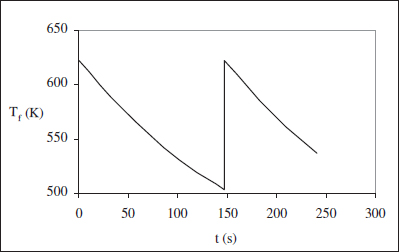
Figura 3.5. Evolució de Tf durant una reacció endotèrmica en un RDTA.

Exemple 3.4

Calculeu l’àrea o àrees de transmissió de calor necessària i les corbes temperature del fluid calefactor-grau de conversió-temps, en un RDTA en el qual es desenvolupa una reacció elemental irreversible, en fase líquida, de la forma: A1 → A2.

Dades i Notes. La reacció és endotèrmica, i la seua calor de reacció és a 393 K, de 21000 J/mol. La constant de velocitat val 0.005 s-1. El volum útil del reactor és de 0.5 m3. La mescla que s’introdueix en el reactor conté 5 kmol de A . La temperatura de reacció serà 393 K, i es vol aconseguir un grau de conversió del 70 %. El coeficient global de transmissió de calor val U = 1046 W/m2 K. És acceptable la hipòtesi que es tracta d’un sistema de densitat constant. La calefacció s’efectuarà amb vapor de Dowtherm, la temperatura del qual pot oscil·lar entre 503 i 623 K.

Solució:

Dades: Esquema de reacció A1 → A2, reacció elemental, és a dir, de primer ordre. r = k c1 = 0.005 clo(1 - X) (mol/s L). ΔH = 21000 J/mol (endotèrmica).

Reactor: RDTA isoterm a T = 393 K, V = 500 L, X = 0.70.

Aliment del reactor: Nlo = 5 kmol, per tant clo = Nlo/V = 10 mol/L.

Sistema d’intercanvi de calor U = 1046 W/m2 K, i Tf entre 503 i 623 K.

Model:

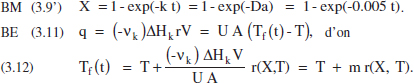
a) Àrea o àrees de transmissió de calor.

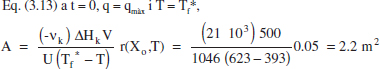
Amb la qual cosa m = 4600 L s K/mol.

Com es pot veure, s’ha fixat com a valor inicial de la temperatura del fluid bescanviador el valor més gran possible. Com que m>0 (reacció endotèrmica) aquesta temperatura anirà disminuint en avançar la reacció:

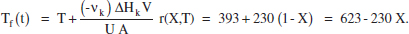
Cal veure si amb aquesta estratègia podem assolir la conversió desitjada (0.70). Per a aquest valor de X, Tf resulta ser 462 K (<Tf*). Per això, cal introduir alguna modificació per tal de poder operar el sistema. Aquesta modificació pot ser blocar una part de l’àrea d’intercanvi (pot tractar-se d’un sistema múltiple d’intercanvi, una de les parts del qual deixa de funcionar en qualsevol moment). Cal determinar, doncs, el moment en què s’ha de canviar de funcionament. Aquest moment serà quan s’assoleix la temperatura inferior per al fluid bescanviador.

Amb l’equació anterior, per a Tf = 503 es té X = 0.52. Aquesta conversió s’assoleix en:

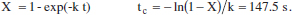
Si decidim que la temperatura en el moment del canvi assoleix de nou el seu valor màxim, la nova àrea serà:

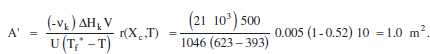
És a dir, cal blocar 1.2 m2. Amb la qual cosa m’ = 9583 L s K/mol.

b) Perfil Tf - X - t.

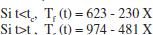
I, en tot cas, la variable temps vindrà donada per t = - ln(l - X)/k. Els resultats es poden veure en la figura 3.5.

3.3.4 Producció

Aquest sistema funciona per cicles. Cada cicle pot considerar-se format per les etapes següents: neteja i condicionament, ompliment, reacció i buidatge. Cada etapa consumeix una part del temps total del cicle. A més a més, només una d’aquestes etapes (la de reacció) pot considerar-se directament productiva, per això les altres es tracten com a temps mort (t’), encara que necessari:

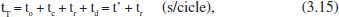
on to és el temps de Fetapa de neteia i condicionament, t el de la de càrrega, etc. La relació existent entre el volum de reacció (un o diversos reactors funcionant de la mateixa manera) i el cabal de producció (m3 de la mescla reactiva/s) serà:

El flux molar de producte obtingut (suposant que a t = 0 no hi ha producte) serà

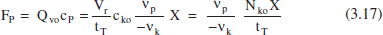
L’equació (3.17) facilita el càlcul del temps de reacció que correspon a la màxima producció, la qual cosa és una informació interessant. Per a valors xicotets d’aquesta variable (tr) normalment es tenen valors grans de la velocitat de reacció, però encara s’aconsegueixen valors xicotets de X, de la concentració de producte i de la producció. Aquesta última per la importància de f’ enfront de tr. Al contrari, per a valors grans de tr es tenen valors xicotets de la velocitat de reacció, encara que X siga gran. El valor gran del temps farà que la producció siga reduïda. Pareix raonable que hi haja algun valor intermedi per al qual Fp siga màxima:

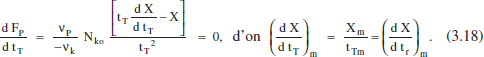
Això pot visualitzar-se gràficament tal com es mostra en la figura 3.6.

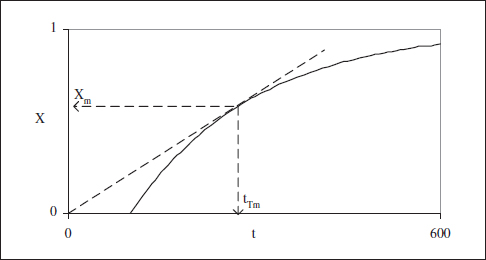
Figura 3.6. Condicions de producció màxima.

3.4 RFP

3.4.1 Sistemes d’intercanvi de calor

Ateses les característiques d’aquest reactor, els sistemes d’intercanvi seran externs, és a dir, Fintercanvi de calor tindrà Hoc a través de la paret. Els sistemes d’intercanvi seran: camises, resistències enrotllades, forns, etc.

on Tf = f(l), és a dir, la temperatura del fluid bescanviador ha de canviar d’una manera determinada al llarg del reactor per tal d’aconseguir el comportament isoterm. As és l'area d’intercanvi per unitat de longitud de reactor (és a dir, el perfmetre).

3.4.2 Relació X-τ(Qvo, V), per a distintes cinètiques

Per a comprovar una vegada més l’equivalència entre aquest reactor i el RDTA, com correspon a la similitud dels models matemàtics, amb els canvis de les variables respectives τ per tr, es mostrarà l’aplicació del model del balanc. de matèria a una cinètica de primer ordre. Suposem que es tracta d’un sistema de densitat constant. Reacció: A → productes r = k cA.

Aplicant el balang de matèria, equació (2.58),

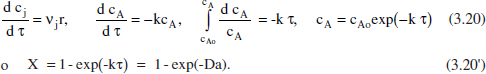
Equacions equivalents a les (3.9). En el capítol 3 de l’Omnibook de Levenspiel (1993) es poden consultar les aplicacions d’aquests balangos a altres cinètiques. En lay taula 3.1 es comparen algunes de les equacions obtingudes per a distintes cinètiques i els diferents reactors ideals.

3.4.3 Flux de calor intercanviat

Per a calcular el flux de calor [q = f(l) = f(V) = f(x)] necessari per a mantenir el comportament isoterm s’utilitzarà el balanc. d’energia combinat amb el de matèria. Així, de l’equació (2.79):

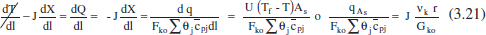
Com que r variarà amb la composició (excepte si la reacció és d’ordre zero), i aquesta ho fa amb la posició, q (és a dir, la parella U-Tf o bé qA) s’haurà d’adaptar a aquesta evolució. Per això, la solució del balang de matèria ens informarà de la variació de la composició (X) al llarg del reactor (l o τ), i l’equació (3.21) ens permetrà calcular el valor de q que cal intercanviar en cada posició del reactor.

3.4.4 Producció

Ací es poden repetir, amb algunes diferències, els comentaris efectuats per al RCTA. Conegut X, es pot calcular Fp, o deixar Fp en funció del volum del reactor. Per a un sistema amb una sola reacció, volums grans de reactor i velocitats de reacció grans permetran obtenir una elevada producció.

Exemple 3.5

El Departament de Màrqueting de l’empresa on treballes ha determinat que es poden col·locar en el mercat 1260 tones/any d’un producte C (darrere d’aquesta denominació s’amaga un producte important, utilitzat en la fabricació d’una no menys important fibra). El reactor que s’haja d’utilitzar en aquest procés estarà operatiu 24 h/dia i 350 dies/any.

A fi d’estudiar algunes de les possibles alternatives es plantegen les qüestions següents:

a) Si la reacció es desenvolupa en un RCTA, estudieu la influència del cabal volumètric sobre el volum de reacció necessari. Amb aquest objectiu, determineu el volum d’aquest reactor per a, almenys, quatre cabals possibles i diferents. A la vista del model proposat i dels resultats obtinguts, hi ha algun cabal mínim per davall del qual no es pot aconseguir la producció desitjada?

b) Repetiu l’apartat anterior per al cas que el reactor que s’utilitze siga un RFP.

c) Si el procés es porta a terme en un RDTA ideal, on el temps de càrrega, descàrrega i neteja és de 2 h, analitzeu la influència de la conversió assolida en el reactor sobre el volum de reactor necessari. Per a això, calculeu el volum de reactor que es necessita per a quatre (com a mínim) valors del grau de conversió. A la vista dels resultats, creieu que hi ha algun grau de conversiótemps de reacció òptim?

Dades i Notes. El pes molecular de C és 50. La reacció té Hoc en fase líquida i es correspon amb l’estequiometria: A + B → C. La cinètica de la reacció, atès que s’utilitza un gran excés de B, pot aproximar-se a una de primer ordre. La constant de la velocitat de reacció, en les condicions d’operació, val 0.005 min-1. L’aliment de què es disposa té una concentració en A de 0.2 mol/L.

Solució:

La producció desitjada de C és 1260 tones/any = 50 mol/min = Fc. cAo = 0.2 mol/L.

a) Relació V-Qv per a un RCTA.

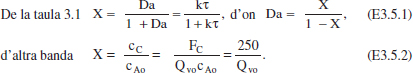
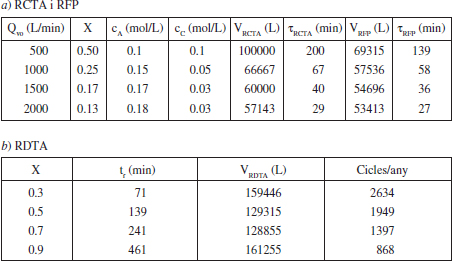
Els valors permesos de Qvo són aquells que condueixen a valors de X raonables. Com que 0 ≤ X ≤ 1, aleshores 250 ≤ Qvo. Cabals inferiors no permetrien assolir la producció desitjada. En la taula E3.5 es mostren alguns resultats de la conversió per a diferents cabals. Per a cada valor de Qvo amb (E3.5.2) calculem X, i amb (E3.5.1) Da, τ i V.

b) Relació V-Qv per a un RFP.

De la taula 3.1

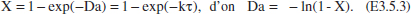
L’equació (E3.5.2) és vàlida també en aquest cas, per la qual cosa els valors permesos de Qvo són 250 < Qvo. En la taula E3.5 es mostren alguns resultats de la conversió per a diferents cabals. Per a cada valor de Qvo amb (E3.5.2) calculem X, i amb (E3.5.3) Da, τ i V. Com que es tracta d’una reacció de primer ordre (ordre positiu) el volum necessari d’un RCTA és més gran que el d’un RFP, encara que les diferències es redueixen en ausmentar Qvo i disminuir X.

c) Relació V-X per a un RDTA.

De la taula 3.1

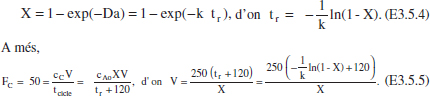
Donant valors a X, calcularem el del volum necessari; alguns resultats es mostren en la taula E3.5. Cal adonar-se que tr = τRFP, per al mateix X. Es pot veure que hi ha un mínim, per a determinar-lo fern dV/dX = 0, d’on X = 0.6 i V = 126353 L.

TAULA E3.5

Disseny d’un reactor per a desenvolupar la reacció A + B →C

3.5 Selecció del tipus de reactor i de les condicions d’operació. Temperatura òptima (o perfil òptim de temperatura)

En aquest capítol s’ha considerat el funcionament isoterm dels reactors. Cal preguntar-se, quan interessarà que el reactor funcione d’aquesta forma?, i d’una forma més general, quines són les condicions òptimes de funcionament d’un reactor?, i quin és el reactor més adequat per a una reacció donada? Des d’un punt de vista netament acadèmic, pot semblar que l’elecció, tant del tipus com del disseny òptim del reactor, hauria de sorgir d’un estudi ben organitzat de totes les possibilitats. Encara que els ordinadors poden ajudar en aquest atac massiu de tots els problemes possibles, la falta de dades específiques i els límits pràctics de les diferents maneres d’operar suggereixen que una recerca completa de l’òptim quantitatiu no és ni necessària ni raonable. Es pot argüir que d’aquesta forma s’està limitant l’acte creatiu del disseny. No obstant això, cal pensar que aquestes limitacions poden ser bastant àmplies, i que, en tot cas, el dissenyador sempre pot decidir botar-seles, fent ús dels seus coneixements i de la seua llibertat de creació.

D’acord amb l’anterior, en el disseny d’un reactor químic s’han de consi-derar les recomanacions següents:

a) Analitzar les característiques específiques del sistema de reacció. El dissenyador ha de reunir el coneixement existent sobre la naturalesa del sistema de reacció. Aquests coneixements estaran relacionats amb els aspectes següents:

Químic. El coneixement profund dels aspectes químics relacionats amb la reacció (estequiometria, mecanisme de la reacció, reaccions competidores, etc.) és de gran rellevància amb vista al disseny i operació del reactor.

Termodinàmic. Aspectes com la calor de reacció, la conversió d’equilibri i la seua relació amb les condicions de pressió i temperatura són de gran ajuda en la decisió de l’interval d’operació. Així mateix, els aspectes termodinàmics són també necessaris en l’anàlisi de la perillositat del procés.

Model cinètic. En el disseny d’un reactor industrial es necessitarà el model cinètic de la reacció, o almenys una sèrie de dades bàsiques per a l’escalatge.

Propietats físiques de reactius i productes. Aquestes informacions són necessàries per a càlculs detallats del disseny, però també per a poder comprendre les característiques de flux, de la transferència de calor i de la manejabilitat d’aquests. S’han de determinar els possibles problemes toxicològics, etiològics i ecològics.

Característiques del catalitzador, si n’hi ha. Cal conèixer tant les característiques físiques com químiques del catalitzador, amb especial menció al valor límit de la temperatura, possibles verins i manteniment de la seua activitat.

b) Basant-se en els factors analitzats en el punt a, seleccionar les condicions d’operació que fan mínima la grandària del reactor i/o màxim el rendiment en el producte desitjat. El cost de les etapes de separació i recirculació és sovint de gran importància en la selecció dels nivells de conversió.

c) A partir dels factors considerats en els punts a i b, seleccionar el tipus de reactor ideal i el procediment d’alimentació que condueixen al mínim cost del reactor i/o al màxim rendiment en el producte desitjat.

d) Seleccionar el tipus de transferència de calor d’acord amb les conclusions dels punts anteriors.

e) Eliminar qualsevol tipus de reactor que puga crear problemes de seguretat que no es puguen controlar d’una manera raonable.

f) Seleccionar un reactor real que s’aproxime tant com siga possible al reactor ideal seleccionat i a les seues condicions d’operació. Els processos de transport s’han de considerar en aquest punt.

g) Calcular la grandària i el comportament del reactor per a les condicions de disseny, considerant simultàniament tant els processos físics com els químics. Diversos dissenys alternatius poden ser considerats, i els aspectes econòmics analitzats acuradament.

h) Buscar els esquemes d’operació òptims, i considerar possibles canvis en la qualitat i quantitat de l’aliment. Analitzar l’operativitat del disseny proposat en relació amb possibles errors en les dades físiques i químiques. Un programa per al disseny d’un reactor pot ser fàcilment adaptat a un programa d’operació, que permeta al dissenyador considerar diversos canvis possibles en les condicions, a fi de comprovar la flexibilitat del disseny. D’aquesta manera s’obtindrà un disseny millorat, que garantirà l’operativitat des d’un ampli ventall de condicions.

Vegem, doncs, la selecció de les condicions d’operació per a reaccions aïllades:

1. Temperatura i pressió:

– Operar per damunt del punt de condensació per a reaccions gasoses, i entre la temperatura de liqüefacció i la de vaporització per a reaccions en fase líquida.

– Operar en l’interval que afavoreix aconseguir la màxima conversió en l’equilibri.

2. Temperatura:

– Seleccionar la temperatura més alta per a reaccions endotèrmiques i exotèrmiques irreversibles. Aquesta temperatura coincidirà amb la temperatura límit establida considerant els costos del reactor i d’operació, la vida del catalitzador i la seguretat.

– L’interval de temperatures ha d’estar fora de la zona on les reaccions laterals són significatives.

– Les reaccions exotèrmiques reversibles i algunes catalítiques irreversibles presenten màxims en la velocitat de la reacció en funció de la temperatura. D’aquesta manera, es pot establir un perfil ideal de temperatures i buscar aproximacions pràctiques a aquest perfil.

3. Pressió (reaccions en fase gas):

– La conversió d’equilibri de les reaccions reversibles que presenten augment en el nombre de mols es veu afavorida per baixes pressions, però açò pot reduir la velocitat de la reacció. Un perfil decreixent de pressió pot ser útil.

– Pressions elevades acceleren la velocitat de reacció, afectant al mateix temps l’equilibri. No obstant això, la majoria de les reaccions industrials operen per davall de 1000 atm (la principal excepció és el polietilè d’alta pressió, que opera a pressions de prop de 2000 atm). L’augment del cost de l’energia accelerarà la tendència habitual cap a les alternatives de baixa pressió per als processos existents.

– Evitar els intervals de pressió que poden donar lloc a reaccions laterals de manera significativa.

4. Concentració i relació de concentracions:

– Elevades concentracions en reaccions en fase líquida eleven la velocitat de reacció, però poden produir augments en el cost de la recuperació i de la recirculació.

– La dilució dels reactius amb inerts pot produir, en alguns casos, la desaparició d’algunes reaccions laterals i ajudar al control de la temperatura.

– L’excés d’un reactiu en un sistema de dos reactius és a vegades atractiu perquè pot produir elevades velocitats de reacció. Açò és especialment útil per a reaccions reversibles en què l’excés d’un reactiu assegura la continuïtat en velocitats importants en produir-se els productes.

– En aquelles reaccions que es troben pròximes a l’equilibri, es pot obtenir un augment en la conversió eliminant contínuament alguns dels productes. Si aquest producte és volàtil o immiscible aquesta tècnica és bastant atractiva. Les reaccions laterals reversibles no desitjades poden eliminar-se recirculant al reactor els productes d’aquestes reaccions.

Si ens centrem de moment en la temperatura, que és l’elecció que fem en aquest capítol, vegem amb un poc més de detall el que s’acaba de dir. D’acord amb els diagrames r-X-T vistos en el capítol anterior es pot deduir el valor òptim de la T (RCTA) i el perfil òptim de temperatures (RDTA i RFP). Lògicament, interessarà disposar de velocitats de reacció elevades, la qual cosa sol portar associat temperatures elevades. També pareix raonable que hi haja algun valor màxim d’aquesta variable (T*). Aquest valor límit pot venir fixat per les nostres limitacions en relació amb la capacitat de bescanvi de calor, o perquè per damunt d’aquesta temperatura apareixen problemes en el sistema reactiu (aparició d’alguna reacció que competeix amb la reacció que ens interessa, o que fa desaparèixer el producte). La seguretat del procés és un altre criteri per a fixar T*.

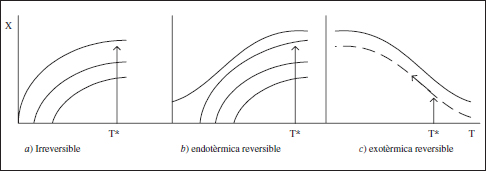
La temperatura (o perfil de) òptima (figura 3.7) per a una reacció irreversible o una d’endotèrmica reversible és T = T*, mentre que per a una reacció exotèrmica reversible serà T = T* fins a arribar a Γm, i després caldrà seguir Γm. En conseqüència, es pot dir que el comportament isoterm és interessant per a algunes de les possibles reaccions.

Figura 3.7. Perfil òptim de temperatura.

Qüestions, problemes i lectures d’ampliació

Qüestions

1. Un aliment gasós entra en un reactor a 720 K i 1.2 atm, amb les següents concentrations (mol/L) 100 de A, 150 de B, 50 de R i 100 de I (inert). En el reactor té Hoc la reacció A + 3 B → 2 R. El gas d’eixida passa per un refrigerant i abandona el sistema a 300 K i 1 atm, amb una concentració de A de 160 mol/L. Determineu les concentrations de les altres espècies a l’eixida i el grau de conversió referit al component A.