- -
- 100%
- +
Anote dos ejemplos: ........................................
3. Números racionales
¡Dividir es repartir en partes iguales!
Un grupo de 6 amigos juega a las cartas con un mazo de 52 cartas.
El juego consiste en repartir todas las cartas y dejar el resto en el centro de la mesa. ¿Cuántas cartas le corresponden a cada uno? ¿Cuántas cartas quedan en el centro?
¡Tú puedes deducir la respuesta!
DEFINICIÓN: son los que se pueden escribir como el cociente de dos enteros. Se pueden expresar como fracción.
EN SÍMBOLOS:
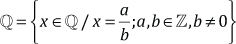
Los números racionales representan partes de un todo.
También, los números racionales, se caracterizan por su expresión decimal:

Las partes sombreadas de los siguientes objetos están representadas por números racionales.
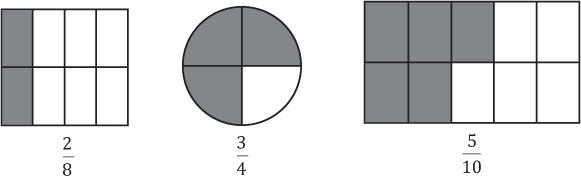
Observe que:
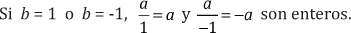
Entonces «Todos los enteros son racionales». Es decir
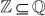
Notación decimal
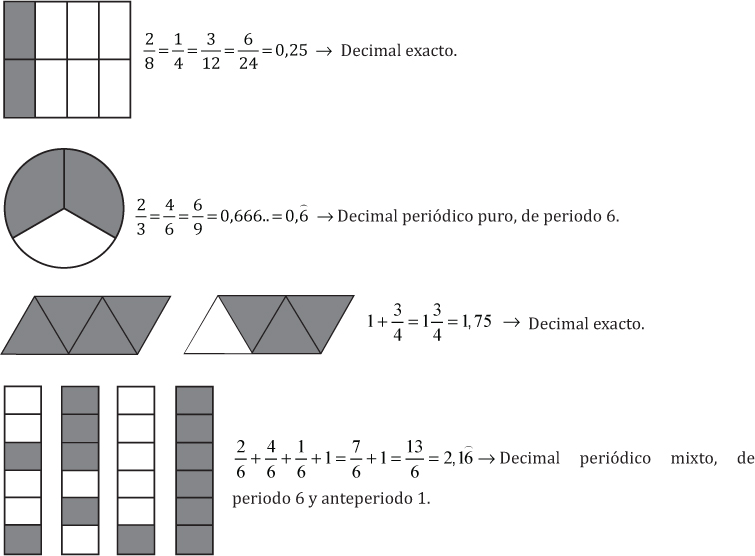
Todo número racional puede expresarse en notación decimal ya sea exacta o infinita periódica.
Cada número racional expresado en notación decimal está compuesto de dos partes:

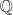
Entre dos números racionales hay infinitos números racionales. Esta afirmación podría justificarse sencillamente si tenemos en cuenta que la suma de racionales es siempre otro racional, el promedio será otro racional y estará comprendido entre ellos.
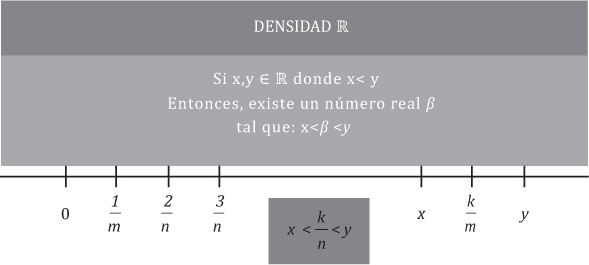
Podríamos continuar indefinidamente el procedimiento de promediar dos números racionales, encontrando siempre que hay otro racional entre dos racionales, por más próximos que estén. Por ello decimos que Q es un conjunto denso.
Actividad 1.3:
Indique si las siguientes afirmaciones son verdaderas o falsas. Justifique.
1.
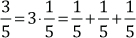
( )
2.
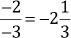
( )
3.
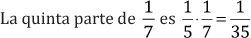
( )
4.

( )
4. Números irracionales
Todos los números racionales están representados por puntos sobre la recta numérica, pero ¿todos los puntos de la recta son representaciones de números racionales? La respuesta es NO. Existen otros números que junto a los números racionales completan a la recta numérica: los números irracionales.
DEFINICIÓN: Los números irracionales son los que no se pueden expresar como fracción. En símbolos:
I = {x / x no se puede expresar como fracción
Convertidos a la notación decimal son números con infinitas cifras no periódicas.
SIMBÓLICAMENTE:
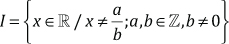
Ejemplos:
Los siguientes son números irracionales famosos. Están redondeados en la quinta cifra decimal, con lo cual se obtiene un valor aproximado bastante aceptable.
a. El número PI: = π ≈ 3,14159
b. El número e ≈ 2,71828
c. El número de oro:
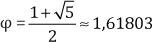
d. Raíces no exactas como son:
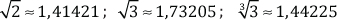

PI (π): es la relación que existe entre el perímetro y el diámetro de una circunferencia. Quiere decir que si divides el perímetro por el diámetro de cualquier circunferencia resulta el número π.
El número π tiene un valor de: 3,14159265…
Este número es de los más utilizados en matemáticas, física e ingeniería porque la circunferencia es un elemento muy común.
Ubicación exacta de
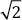
Con ayuda del Teorema de Pitágoras podemos ubicar de manera exacta el número
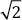
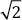
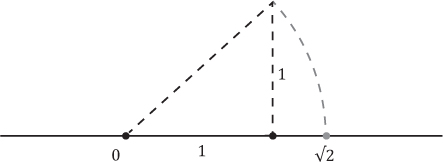

Teorema de Pitágoras
En todo triángulo rectángulo se cumple que el cuadrado de la medida de la hipotenusa es igual a la suma de los cuadrados de las medidas de los catetos.
Una operación en I es una manera de asociar a cada par de números irracionales, otro número irracional bien determinado. Las operaciones que se definen en este conjunto son la suma, la resta, la multiplicación, el cociente y la extracción de raíces (exceptuando la radicación de números negativos de índice par).
Las operaciones de suma, diferencia, producto, cociente y potenciación de números irracionales no siempre arrojan como resultado a otro irracional. Algunas veces los resultados son racionales.
5. Números reales
DEFINICIÓN: el conjunto de los números reales surge de la unión de los números racionales y de los irracionales. Se denota como
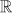
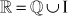

Se habla del orden en los números reales a través de la propiedad de tricotomía afirmando que dados n y m dos números reales, entonces se tiene exactamente una de las tres posibilidades:

Al igual que en los conjuntos
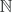

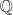
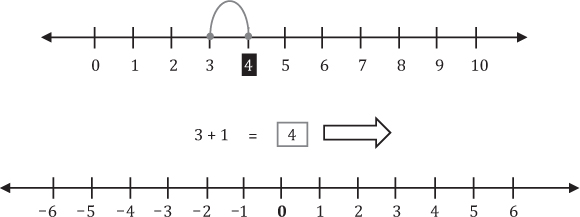
La recta
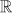
En general, dado un punto P cualquiera en la recta, al número real a se le llama coordenada o abscisa de P y se denota por P(a), que se lee: punto P de coordenada a.
Ejemplo:
Ubiquemos de forma aproximada los siguientes números en la recta real:
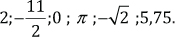
Solución
En forma de coordenadas, los números toman la forma:
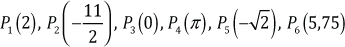

Una operación en
• La división entre cero.
• La extracción de raíces de índice par de números negativos.
Propiedades Básicas
Potenciación
Si a es un número real y n es un número natural, entonces decimos que an se obtiene multiplicando n veces el factor a, es decir:
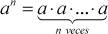
Ejemplo:
a6 = a. a. a. a. a. a. a
Decimos entonces que an es una potencia que tiene a como base y n como exponente. Extendemos la definición para exponentes enteros definiendo, para a ≠ 0;

Actividad 1.4:
Indique si los siguientes enunciados son verdaderos o falsos:
a. 28 = 22. 26 = 25. 23
( )
b. (8+3)2 = 82 + 32
( )
c. (8.3)2 = 82 + 32
( )
d. (23)2 = 35
( )
e. (23)2 = 26
( )
f. – 32 = (–3)6
( )
g. 54 = 45
( )
h.

( )
i. 5–2 = –10
( )
La actividad anterior ejemplifica algunas de las siguientes propiedades de la potencia: Sean a, b números reales distintos de 0 y sean m, n números enteros.
Propiedades de la PotenciaDistributiva con respecto al producto(a · b)m = am · bmDistributiva con respecto a la división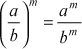
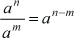
Observación:
Como se apreció en el ejercicio anterior, la potencia no es distributiva con respecto a la suma ni a la resta.
• ¿Qué sucede si a un número negativo lo elevamos a una potencia par? ¿Cuál es el signo del resultado?
• ¿Existe alguna potencia de 5 que dé como resultado un número negativo? ¿Por qué?
Radicación
Para los enteros positivos n, ya se ha definido la n-ésima potencia de b, a saber, bn. Ahora, vamos a utilizar la ecuación a = bn para definir la n–ésima raíz de a.
En general, la raíz cuadrada de a se define como sigue. A veces recibe el nombre de raíz cuadrada principal de a
Si a es un número real positivo,
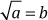
Además,

Ejemplo:
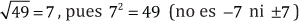
Actividad 1.5:
Calcule el valor de cada una de las expresiones que siguen, en caso de estar definidas:
a.
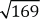
b.
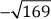
c.

En el caso de las raíces cúbicas se puede utilizar tanto números positivos como negativos, así como el cero. Por ejemplo:
23 = 8 y (–5)3 = –125
Se puede decir entonces que:
Si a y b son números reales cualesquiera,
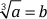
Ejemplos:

Se puede ver que existe una diferencia básica entre las raíces cuadradas y las raíces cúbicas. Las raíces cuadradas están definidas solo para los números reales positivos y el cero. Las raíces cúbicas están definidas para cualquier número real.
Observaciones:
•


• El número a es el radicando,
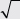

Veamos ahora las propiedades de la radicación, las cuales son análogas a las de la potenciación.
Sean a, b números reales positivos y n, m números naturales:
Propiedades de la RadicaciónDistributiva con respecto al producto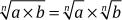
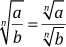
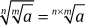
Actividad 1.6:
• Al igual que con la potenciación, la radicación no es distributiva con respecto a la suma ni a la resta. Proponga ejemplos que muestren que la propiedad distributiva no se cumple.
• ¿Qué sucede al aplicar la propiedad distributiva al siguiente radical:
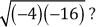
Orden de operaciones
Orden de operaciones sin símbolos de agrupación o colección
Para calcular expresiones numéricas en las cuales no hay símbolos de agrupación (paréntesis, corchetes o llaves), se opera en el siguiente orden:
1. Potencias y raíces.
2. Multiplicaciones y divisiones.
3. Adiciones y sustracciones.
Si hay dos operaciones de la misma jerarquía, se opera de izquierda a derecha.
Ejemplo: 10 + 12 ÷ 3 × 2 = 18
Ejemplo: 10 + 12 / 3 × 2 = 14,6666
Orden de operaciones con símbolos de agrupación o colección
Si la expresión numérica contiene símbolos de agrupación como paréntesis, corchetes y llaves, se efectúan, primero, las operaciones indicadas dentro de los símbolos de agrupación, empezando por los interiores y respetando la jerarquía de operaciones.

Trabajemos en clase
1. Complete con los símbolos ∊, ∉, ⊆ o ⊆ según corresponda.

2. Dado el conjunto
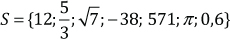

Represente el conjunto S en la recta numérica en forma aproximada.
3. Desarrolle:
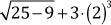
4. Calcule el valor de:
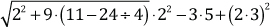
5. Solucione:


Ejercicios y problemas
Manejo de conceptos
1. Indique si las siguientes afirmaciones son verdaderas o falsas y justifique sus respuestas.
a. La suma de dos números naturales es siempre un número natural.
( )
b. La diferencia de dos números naturales es siempre un número natural
( )
c. El cuadrado de un número racional negativo es un número racional positivo.
( )
d. Existen infinitos números racionales comprendidos entre 0 y
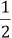
( )
e. El conjunto de los números naturales carece de primer elemento.
( )
2. Indique si las siguientes afirmaciones son verdaderas o falsas. Justifique la respuesta proponiendo un contraejemplo, en caso de ser falsa, o enunciando las propiedades aplicadas, en caso de ser verdadera.
a. Si a = –2 y b = 0, entonces a : b = 0
( )
b. (–a) · (–b) = (a . b)
( )
c. El cociente entre un número y su opuesto es igual a –1
( )
d. a + (– b + c) = a – b + c
( )
e. El inverso de 2 es 12
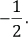
( )
f. a: (b + c) = a:b + a : c, siendo b + c ≠ 0, b ≠ 0 y c ≠ 0
( )
g. b – [–c · (2 – 1) – 1] = b
( )
h. a – (b + c) = a – b + c
( )
i. (b + c): a = b: a + c, con a ≠ 0
( )
j. Para todo a ∈
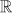
( )
k. Para todo a ∈
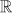
( )
l. a · (–b) = a · b
( )
m. a · (b – c) = a · b – a · c
( )
n. La ecuación 2x = 1 tiene solución en

( )
o. –(– a) = a
( )
Habilidades de cálculo
1. Responda:
a. Si m = 14, ¿cómo pueden representarse los números 13; 15 y 16 en términos de m?
b. Sea n un número par cualquiera, ¿cuál es el siguiente entero par? ¿Cuál el anterior?
c. Si x representa cualquier entero impar, ¿cuál es el siguiente entero impar? ¿Cuál el anterior?
d. Si x es cualquier entero par, ¿x + 1 es un entero par o impar? ¿y x – 1?
e. Si x es cualquier entero ¿2x es par o impar? ¿y 2x – 1? ¿y 2x + 1?
2. Calcule:

3. Complete con = o ≠ y mencione qué propiedades se cumplen o no se cumplen: