- -
- 100%
- +
a. (a + b)n____an + bn
b. ab____ba
c. abc____(ab)c
d. (p · q)a____pa · qa
4. En los siguientes cálculos se han cometido errores al aplicar las propiedades. Indique cuáles son y corríjalos.
a. (22 · 2–3 · 25)2 = (24)2 = 216
b. (52)4 ÷ (5–3)2 = 5–6 ÷ 5–6 = 50 = 1
c.
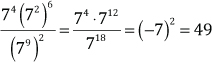
d. (7.2–14)0 + 50 = 2
5. Desarrolle:
Modelación
1. Un semáforo comienza su funcionamiento con la siguiente secuencia y duración: luz roja 4 minutos luego amarilla 3 minutos, finalmente, verde 2 minutos. Si comienza con luz roja a las 12:15 horas, ¿cuál o cuáles de las siguientes afirmaciones es o son correctas?
I. A las 12:25 tiene luz roja.
II. A las 12:30 tiene luz amarilla.
III. A las 12:35 tiene luz verde.
a. Solo I
b. Solo I y II
c. Solo I y III
d. Solo II y III
e. I, II y III
2. Si las letras p y q indican suma 2 y resta 3 respectivamente, entonces, ¿cuál de las siguientes expresiones tiene un mayor valor?
a. 5(1 + p)
b. 3(q + 6)
c. 2(q + 8)
d. 3(p + 4)
e. 10(q + 2)
3. Claudio tiene 8 bolitas más que Juan. Juan tiene 5 bolitas menos que Andrés, y Patricio 3 bolitas más que Andrés. Entonces, ¿cuál o cuáles de las siguientes aseveraciones es o son correctas?
I. Juan es quien tiene menos bolitas.
II. Claudio es quien tiene más bolitas.
III. Claudio tiene 3 bolitas más que Andrés.
a. Solo I
b. Solo II
c. Solo I y II
d. Solo I y III
e. I, II y III
4. ¿En cuántos minutos más serán las 11:45, si hace 20 minutos eran las 9:15?
a. 150 minutos
b. 130 minutos
c. 120 minutos
d. 110 minutos
e. 100 minutos
5. En 14 días más daré mi segunda prueba de Matemática. Si la primera prueba fue 22 días antes que la segunda, hace cuarenta días atrás, ¿cuántos días faltaban para rendir mi segunda prueba?
a. 4
b. 18
c. 32
d. 40
e. 48
6. Si las letras del abecedario representan a los primeros números naturales de menor a mayor respectivamente, entonces es correcto afirmar que:
I. c + c = b × c
II. b×(a + b) = b + c
III. c + a × b = a × b × c
a. Solo I
b. Solo I y II
c. Solo I y III
d. Solo II y III
e. I, II y III
7. La diferencia entre dos números es 8. Si el mayor es cuatro unidades menos que el doble del menor, entonces ¿la suma de los números es?
a. 20
b. 28
c. 30
d. 32
e. 36
8. Si (x2 – 4x + 4) representa el área de un cuadrado, entonces su perímetro queda representado por:
a. x – 2
b. 4x – 2
c. 4x – 8
d. 4x – 16
e. 4x + 8
9. Daniela debe tomar un litro y medio de leche diario. Si con 120 gramos de leche en polvo se hace un litro ¿cuántos kilogramos necesita para 30 días?
a. 4,4
b. 4,5
c. 4,8
d. 5,4
e. 5,6
10. Se envasa arena en sacos de 4 kilos (A) y sacos de 8 kilos (B). Si se debe completar 80 kilos de arena ¿qué combinación de sacos se puede usar?
I. 5A + 5B
II. 12A + 4B
III. 2A + 9B
a. Solo II
b. Solo III
c. Solo I y II
d. Solo II y III
e. I, II y III

Páginas web para consultar
Más ejemplos y ejercicios sobre números reales:http://www.vitutor.com/di/re/r2.html

Números racionales
Lectura introductoria a los Números racionales. Historia de los camellos

Un viejo pastor que sabía que se moría, tenía como fortuna 17 camellos que había alquilado a los conductores de caravanas. Vivía con sus tres hijos Hussein, Hassan y Hassin ¿qué sería de ellos?, se preguntaba con preocupación. Sabía que sus hijos aunque buenos y trabajadores, eran muy peleones. Una tarde cuando caía la noche, el viejo reunió a sus tres hijos y les dijo:
—Atended hijos míos. Yo sé que no estaré ya mucho tiempo con ustedes, recordad esto: vuestra riqueza son los 17 camellos que les dejo. Vosotros los repartiréis de la siguiente forma: Tu Hussein, eres el mayor, como has trabajado mucho tiempo conmigo te dejo la mitad de mi manada. A ti Hassan, el menor, que has trabajado también conmigo, pero menos tiempo, te dejo la tercera parte. Y en cuanto a ti Hassin, que eres el pequeño y no has tenido tiempo de trabajar conmigo, te doy la novena parte. ¿Respetaréis mi última voluntad?—
—Te lo prometemos padre—
A la mañana siguiente, el viejo pastor murió y sus hijos lo enterraron en el desierto. Después se pusieron a pensar en el reparto de la manada. Se acordaron bien de lo que su padre les había dicho, pero no llegaron a encontrar la forma de repartir diecisiete camellos en dos, ni en tres ni en nueve.
—Nuestro padre nos ha metido un gran lío. La mitad de diecisiete camellos es ocho y medio— dijo uno de los hermanos.
—Se puede matar o venderlo a uno y repartir el precio en tres. También podemos esperar hasta que las camellas tengan camellitos. Sí, pero ¿si se muere una camella?—
Los tres hermanos no llegaban a salir del embrollo. Entonces, vieron llegar a un hombre montado en un viejo camello pelado del todo, que les pedía hospitalidad para la noche
—Es Dios quien te envía— le dijo Hussein —Tú podrás darnos un consejo—. Y le explicó el problema del reparto. El viajero escuchó atentamente, reflexionó en silencio y después respondió:
—Hay una solución. Yo os doy mi camello. Así serán dieciocho camellos y podréis hacer el reparto—.
Entonces, hicieron el reparto. Hussein tomo la mitad, es decir, nueve camellos. Hassan la tercera parte, es decir, seis camellos y Hassin la novena parte, es decir, dos camellos. Por la mañana, feliz de haber encontrado la solución, el viajero sobre su viejo camello pelado, el camello 18, continuó su camino.
DE LA CRUZ, Armando (2012). Separata de Números Racionales. Lima: IEP «EDUARDO PALACÍ».
Objetivos:
• Identificar y representar gráficamente los números fraccionarios.
• Organizar estrategias para resolver operaciones combinadas con los números racionales.
• Matematizar situaciones concretas en las que se presentan números racionales.
Ampliación del campo numérico
Analizaremos porqué las operaciones indicadas son posibles de realizar en los respectivos campos numéricos.
Como se estudió anteriormente, en el conjunto de los números naturales, solo eran posibles las operaciones de la adición, la multiplicación y la potenciación, por que cumplen la Ley de Cierre o Clausura.
Al incorporar los números negativos, se resolvió el problema de la resta cuando el minuendo es menor que el sustraendo.
A continuación, estudiaremos la ampliación del campo numérico para resolver el problema de la división, cuando el dividendo no es múltiplo del divisor.

El esquema anterior se expresa, gráficamente, en el siguiente diagrama.
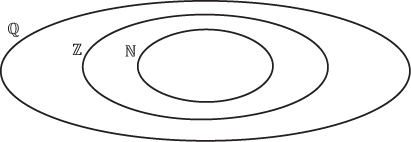
Necesidad de la creación de los números fraccionarios
Los números fraccionarios se crearon para solucionar la división, cuando el dividendo no es múltiplo del divisor.
Ejemplos:
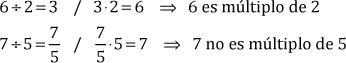
Conjunto de números racionales
El conjunto de los números racionales está formado por el conjunto de los números enteros, unido con el de los números fraccionarios (F).
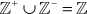
A los números racionales se los designa con la letra
Al incorporar los números negativos, se resolvi

A los números racionales se los designa con la letra
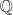
Número racional
Definición: se llama número racional a todo número que puede ser expresado como una fracción.
Ejemplos:
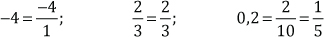
Representación de los números racionales en la recta numérica
A todo número racional le corresponde un punto en la recta numérica, pero no todos los puntos de la recta numérica corresponden a números racionales.
Esto significa que existe una correspondencia unívoca entre los puntos de la recta numérica y el conjunto de los números racionales.

Los números racionales positivos se representan a la derecha del cero, los racionales negativos a la izquierda del cero.
Para representar en la recta números fraccionarios se divide la unidad en tantas partes como indica el denominador y se toman tantas como indica el numerador.

Relación entre números fraccionarios y números decimales
Como se sabe, las fracciones se utilizan para expresar cantidades que no son números enteros. Pero en la práctica, para indicar esas cantidades es frecuente emplear números decimales.
Por ejemplo, decimos 0,6 m en vez de

También debemos recordar que toda fracción es un cociente indicado entre dos números enteros, por lo tanto, a cada fracción le corresponde un número decimal que es el resultado de la división entre el numerador y el denominador.
Actividad 1.7:
• Complete la siguiente tabla:

Teniendo en cuenta las expresiones decimales obtenidas, se observa que existen dos tipos de números decimales.
1. Números cuya parte decimal es finita o limitada, que se denominan números decimales finitos.

2. Números cuya parte decimal es infinita periódica o ilimitada periódica se denominan números decimales periódicos.
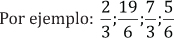
Conclusión
• Toda fracción que tiene en el denominador, potencias de 2, de 5 o producto de ambas potencias, se transforman en números decimales exactos o finitos, es decir, con un número exacto de cifras decimales.
Toda fracción que tiene en el denominador, factores que no sean potencias de 2 o de 5, se transforman en expresiones decimales periódicas.
Actividad 1.8:
1. Escriba los siguientes números indicando cuál es su período:
a.
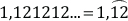
b. 0,151515...=
c. 5,432432...=
d. 123,1312312...=
e. 0,236565...=
f. 0,125125...=
2. Clasifique los siguientes números decimales en exactos, periódicos puros o mixtos:
a. 2,424242
b. 3,25
c.
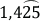
d.

e. 0,42 =
f.

g. –0,4 =
Transformación de una expresión decimal en fracción
Ya se estudió que toda fracción se puede expresar como número decimal. La afirmación recíproca también es válida, es decir que todo número decimal se puede expresar como fracción.
Transformación de un número decimal finito
Para expresar un número decimal finito en fracción, se escribe como numerador, el número dado sin la coma decimal y como denominador, la unidad seguida de tantos ceros como cifras decimales tenga el número dado. Luego se simplifica todo lo posible.
Actividad 1.9:
a. 1,2 =
b. 0,4 =
c. 1,08 =
d. 0,026 =
Transformación de un número decimal periódico
Periódico puro
Para transformar un número decimal periódico puro en fracción, se escribe como numerador el número dado sin la coma decimal y se le resta la parte entera y en el denominador tantos 9 como cifras tenga el período.
Si tiene parte entera se le suma. Luego, se busca la fracción irreducible correspondiente.
Ejemplos:
a.

b.
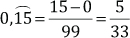
c.

d.
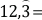
e.
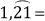
Periódico mixto
Para transformar un número decimal periódico mixto en fracción, se escribe como numerador el número dado sin la coma decimal y se le resta el número formado por la parte entera y las cifras decimales no periódicas y como denominador, tantos 9 como cifras decimales tenga el periodo, seguida de tantos ceros como cifras decimales tenga la parte no periódica.
Ejemplos:

Significado del periodo 9
Ejemplos:
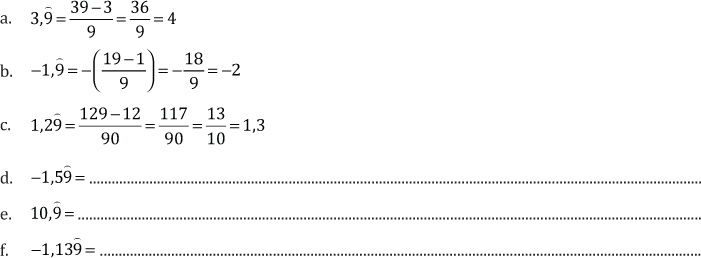
Periodo 9
Cuando en un número decimal periódico, el periodo es 9, se aumenta una unidad a la cifra anterior al periodo, transformándose en un número entero si es una expresión periódica pura, o un número decimal exacto si es una expresión periódica mixta.
Actividad 1.10:
Exprese los siguientes números decimales como fracción irreducible:
a. 1,25 =
b. 1,333...=
c.
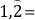
d.
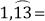
e.
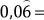
f. 1,33 =
g. 0,05454...=
h.
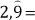
i.

j. 0,75 =
Revisión de operaciones con números racionales
Todas las operaciones que se realizan con números enteros también pueden realizarse con números racionales.
Como a las cuatro operaciones fundamentales (+, –, ×, ÷) se las comienza a estudiar en cuarto año de la escuela primaria, solo se realizará una rápida revisión y se profundizará más, la potenciación y la radicación de números racionales.
Suma y resta de números racionales
Suma y resta de números fraccionarios de igual denominador:

Para sumar o restar números fraccionarios de igual denominador se escribe el mismo denominador y se suman o se restan los numeradores.
Suma y resta de números fraccionarios de distinto denominador:
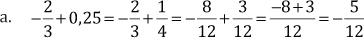
Para sumar o restar números fraccionarios de distinto denominador se buscan fracciones equivalentes a las dadas, cuyo denominador sea el mínimo común múltiplo de los denominadores dados.
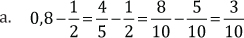
De este procedimiento surge la siguiente regla práctica:
Para sumar o restar fracciones de distinto denominador, se escribe como denominador el mínimo común múltiplo de los denominadores dados, luego este valor se divide por cada uno de los denominadores y a ese resultado se le multiplica por los numeradores. Luego, se suma o se resta, según corresponda.

Suma y resta de números decimales
Para sumar o restar números decimales, se suman o se restan las cifras de igual valor relativo. Para esto, se ubican en columnas las cifras haciendo coincidir la coma decimal.
a. 158,32 – 25,35 = 132,97
b. – 160,12 107,32 =
c. 45,8 – 180 =
Suma y resta de números racionales
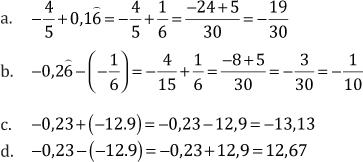
Multiplicación y división de números racionales
Para multiplicar o dividir números racionales se utiliza la misma regla de los signos que se estudió para números enteros.
• El producto (o cociente) de dos números racionales de igual signo es un número racional positivo.
• El producto (o cociente) de dos números racionales de distinto signo es un número racional negativo.
También, para determinar el signo de un producto o cociente de números racionales, podemos expresar la siguiente regla:
• Si la cantidad de factores negativos es par, el resultado es postivo.

• Si la cantidad de factores negativos es impar, el resultado es negativo.
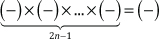
Esta regla explica por qué en
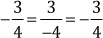
Multiplicación de números fraccionarios

Para multiplicar números fraccionarios, se multiplican los numeradores y los denominadores entre sí, respectivamente. Si se puede simplificar, se realiza antes de multiplicar las fracciones.
Multiplicación de números decimales
a. 0,5 · (–0,02) =
b. 121,3 · (–2,1) =
Para multiplicar números decimales, se operan como si fuesen enteros, luego se coloca la coma según la cantidad total de cifras decimales que intervienen en la operación.
División de números fraccionarios

Para dividir números fraccionarios, se multiplica el dividendo por el inverso multiplicativo del divisor.
División de números decimales
Para dividir números decimales, es necesario que el divisor sea un número entero. Si no lo es, se debe hallar una expresión equivalente para el dividendo y para el divisor, de manera tal, que el divisor se transforme en número entero.
Luego, se divide como si fueran números enteros, colocando la coma decimal cuando se agotan las cifras enteras del dividendo.
Potenciación de números racionales
Potenciación de números fraccionarios
Con exponente natural: para elevar una fracción a una potencia con exponente natural, se eleva numerador y denominador a dicha potencia.
En símbolos:

Ejemplos:





