- -
- 100%
- +
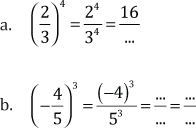
Con exponente negativo: para elevar un número fraccionario a una potencia de exponente negativo, se invierte la base y se la eleva con exponente positivo.
En símbolos:
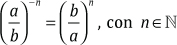
Ejemplos:

Potenciación de números decimales
Para elevar un número decimal a una potencia, se opera como si fueran números enteros, teniendo en cuenta que la cantidad de cifras decimales del resultado es igual al producto entre la cantidad de cifras decimales de la base por el exponente.
Actividad 1.11:
Exprese los siguientes números decimales como fracción irreducible:
a. (0,01)3 = (0,01) · (0,01) · (0,01) =
b. (–0,03)2 = (–0,03) · (–0,03) =
c. (0,08)3 =
d. (–0,002)2 =
Propiedades de la potenciación
La potenciación de números racionales goza de las mismas propiedades que la potenciación de números enteros.

• La potenciación de números racionales es distributiva solamente con respecto a la multiplicación y división.
• La potencia enésima de un producto de varios factores es igual al producto de las potencias enésimas de los factores.
• La potencia enésima de un cociente es igual al cociente entre la potencia enésima del dividendo y la del divisor.
Simbólicamente:

Ejemplos:
Analicemos las siguientes igualdades que verifican la propiedad enunciada anteriormente.
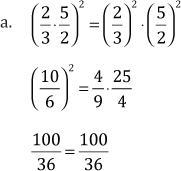
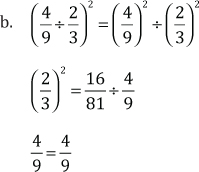
Radicación de números racionales
De números fraccionarios
Para hallar la raíz enésima de un número fraccionario, se halla la raíz enésima del numerador y la del denominador.
Simbólicamente:
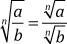
Ejemplos:
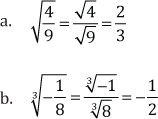
De números decimales
Para extraer la raíz enésima de un número decimal, se opera como si fuera entero, teniendo en cuenta que la cantidad de cifras decimales que se obtiene en el resultado es igual al cociente entre la cantidad de cifras decimales del radicando y el índice.
Actividad 1.12:
Calcule las siguientes raíces aplicando la definición, verificando la regla enunciada anteriormente.

Propiedades de la radicación
La radicación de números racionales goza de las mismas propiedades que la radicación de números enteros.

• La radicación de números racionales es distributiva solamente con respecto a la multiplicación y división.
• La raíz enésima de un producto de varios factores es igual al producto de las raíces enésimas de los factores.
• La raíz enésima de un cociente es igual al cociente entre la raíz enésima del dividendo y la del divisor.
Simbólicamente:

Ejemplos:

Ejercicios combinados con números racionales
Un ejercicio combinado es aquel en el que figuran distintas operaciones matemáticas.
Para resolver un ejercicio combinado, debe respetarse la jerarquía de las operaciones, es decir, el orden de resolución de las operaciones, de la misma manera que con los números enteros.
El orden de resolución de las operaciones es el siguiente:
1. Se resuelven las operaciones que están entre paréntesis y luego las de los corchetes, si los hay.
2. Si no hay paréntesis o corchetes, los signos «+» y «–» separan términos.
Las distintas operaciones que intervienen en un ejercicio combinado, se resuelven en el siguiente orden:
1. Se resuelven las potencias y raíces.
2. Luego las multiplicaciones o divisiones de cada término.
3. Por último las sumas y restas.
4. Siempre se opera de izquierda a derecha.
Ejemplos:
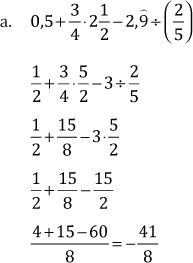

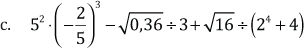

Trabajemos en clase
Desarrolle:
1. Complete con los símbolos ∈ o ∉ según corresponda.

2. Represente en la recta numérica.
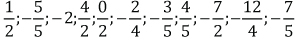
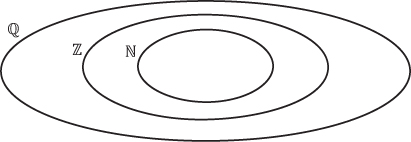
3. Ubique los números del ejercicio 2, en el conjunto numérico correspondiente.
4. Clasifique y transforme en fracción irreducible, los siguientes números decimales.
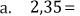
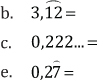
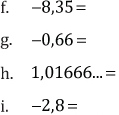
5. Resuelva, expresando los resultados como fracciones irreducibles.
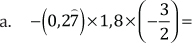
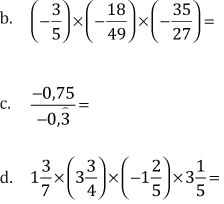
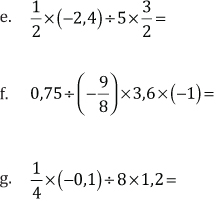

Ejercicios y problemas
Manejo de conceptos
1. Indique si las siguientes afirmaciones son verdaderas o falsas y justifique sus respuestas.
a. La suma de dos números racionales es siempre un número racional.
( )
b. Todo número

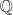
( )
c. Todo número
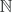
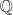
( )
d. La potenciación de números racionales es distributiva con respecto a la adición.
( )
e. Las fracciones que tienen distinto denominador se pueden suman directamente.
( )
f. Si dos fracciones son equivalentes, es menor aquella de menor numerador.
( )
g. Para multiplicar dos fracciones es necesario que tengan el mismo denominador.
( )
h. Todo número decimal también puede ser expresado como como una fracción.
( )
Habilidades de cálculo
1. Coloque los símbolos mayor, menor o igual, según corresponda:
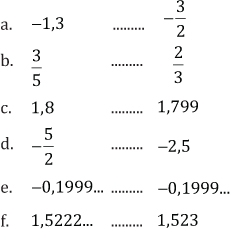
2. Halle el resultado de las siguientes operaciones y escríbalo como una fracción irreducible:
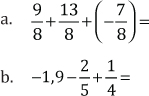
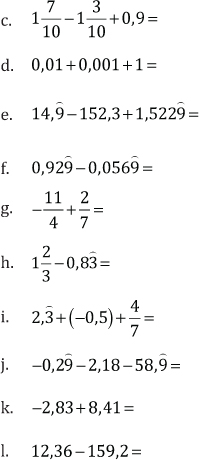
3. Resuelva y exprese los resultados como fracciones irreducibles:
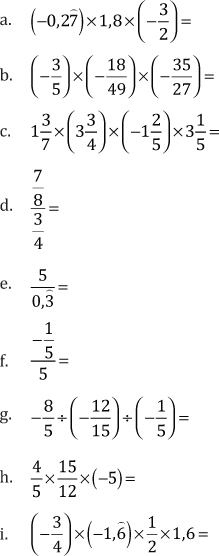
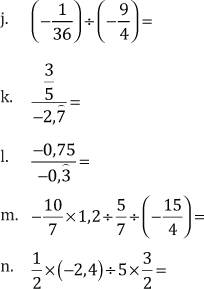
4. Calcule las siguientes potencias:
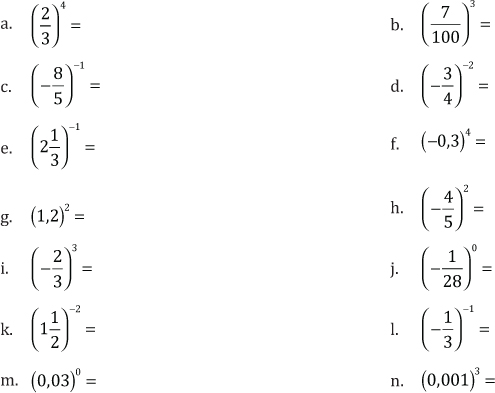
5. Determine, si es posible, las siguientes raíces:
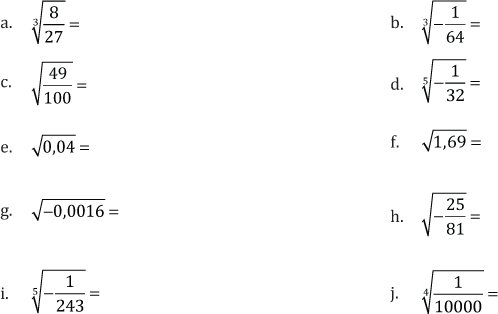

a. En la figura mostrada, ¿qué fracción del rectángulo mayor representa la región sombreada?

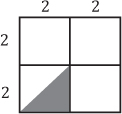
b. La siguiente figura es un cuadrado ¿qué fracción del cuadrado representa la región sombreada?
c. En la siguiente figura:
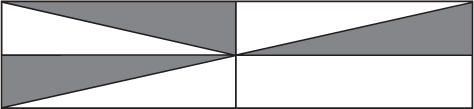
• ¿Qué fracción del rectángulo mayor representa la región sombreada?
• ¿Qué fracción del rectángulo mayor representa la región que quedó sin sombrear?
Modelación
Resuelva los siguientes problemas:
1. Luis invita a sus amigos a comer una torta. Pedro come 1/5, Ana 1/6 y Tomás 1/3. Si Luis se come el resto, ¿cuánto come?
2. De un bidón de aceite se saca primero la mitad y después la quinta parte del resto, quedando aún tres litros ¿cuál es la capacidad del bidón?
3. De su sueldo, el señor Jiménez gastó
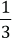
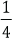

4. Un autor escribió una novela en tres meses. En el primer mes escribió
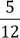
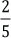
5. La quinceava parte de los alumnos de un curso miran 4 horas de televisión por día, la décima parte mira 3 horas diarias y

6. Se reparte una fortuna entre tres hermanos. El hermano mayor se queda con nueve décimos de los
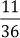
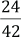
7. Un pintor realiza en el primer día la tercera parte de su trabajo, en el segundo día las


8. Una modista usó

9. En un colegio se eligió la reina que los representaría.

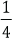
10. El perímetro de un triángulo isósceles es igual a 39 cm. Si cada uno de los lados congruentes es igual a los

11. Durante la primera hora, el dueño de un quiosco de periódicos vendió la cuarta parte de los diarios que tenía, en la segunda hora la sexta parte de lo que quedaba. Contó los ejemplares y le quedaban 25 ¿cuántos diarios tuvo en total?
12. Un avión está dividido en tres categorías de pasajeros: primera clase tiene un octavo del total de asientos, categoría ejecutivo tiene una vez y media de los asientos de primera clase y hay 165 asientos de turistas ¿cuántos asientos tiene el avión?, ¿cuántos asientos de cada clase hay?

Páginas web para consultar
Ejemplos, ejercicios y juegos de fracciones:http://www2.gobiernodecanarias.org/educacion/17/WebC/eltanque/todo_mate/fracciones_e/fracciones_ej_p.html

Razones y proporciones
El hombre de Vitruvio

Leonardo Da Vinci realizó un dibujo llamado «El hombre de Vitruvio» en un diario suyo en el cual representaba a la figura humana vista en dos posiciones sobreimpresas y que está basado en las proporciones del cuerpo humano, es llamado Vitruvio pero con leves desviaciones. Este dibujo está inscrito en un cuadrado de donde sus diagonales se cruzan en los genitales y una circunferencia en la cual el centro se halla en el ombligo del dibujo, pero en la realidad, como media está desplazada ligeramente hacia arriba. El cuadrado y la circunferencia representan al hombre como centro de todas las cosas y es uno de los grandes logros del renacimiento, debido al descubrimiento de las proporciones matemáticas que están aplicadas al dibujo que está hecho en lápiz y tinta, y mide 34,2 x 24,5 cm. Da Vinci realizó este dibujo representando las proporciones del cuerpo humano y, analizando el dibujo en todo su contenido, se descifra que:
Una palma equivale al ancho de cuatro dedos.
Un pie equivale al ancho de cuatro palmas.
Un antebrazo equivale al ancho de seis palmas.
La altura de un hombre son cuatro antebrazos.
Un paso es igual a un antebrazo.
La longitud de los brazos extendidos es igual a su altura.
La distancia entre el nacimiento del pelo y la barbilla es un décimo de la altura de un hombre.
La altura de la cabeza hasta la barbilla es un octavo de la altura de un hombre.
La distancia entre el nacimiento del pelo a la parte superior del pecho es un séptimo de la altura de un hombre.
La altura de la cabeza hasta el final de las costillas es un cuarto de la altura de un hombre.
La anchura máxima de los hombros es un cuarto de la altura de un hombre.
La distancia del codo al extremo de la mano es un quinto de la altura de un hombre.
La distancia del codo a la axila es un octavo de la altura de un hombre.
La longitud de la mano es un décimo de la altura de un hombre.
La distancia de la barbilla a la nariz es un tercio de la longitud de la cara.
La distancia entre el nacimiento del pelo y las cejas es un tercio de la longitud de la cara.
La altura de la oreja es un tercio de la longitud de la cara.
La distancia desde la planta del pie hasta debajo de la rodilla es la cuarta parte del hombre.
La distancia desde debajo de la rodilla hasta el inicio de los genitales es la cuarta parte del hombre.
CHAVES PINTOS, Pablo. (2009) Leonardo Da Vinci. (Consulta: 11 de marzo de 2013). (http://centros.edu.xunta.es/iesramoncabanillas/cuadmat/trabaj/brazo5.pdf)
Objetivos
• Representar simbólicamente razones y proporciones y distinguir sus propiedades.
• Reconocer las diferencias entre magnitudes directamente proporcionales y magnitudes inversamente proporcionales.
• Matematizar situaciones concretas y resolver problemas aplicando las propiedades de las magnitudes directas e inversamente proporcionales.
Razones
La razón consiste en comparar dos cantidades cualesquiera para poder establecer una característica que las relacione, en particular ambas cantidades las podemos comparar principalmente de dos formas: a través de su diferencia (razón aritmética), y mediante su cociente (razón geométrica):
a. Razón Aritmética: es una forma de comparar dos cantidades en las cuales consideramos cuánto excede una de la otra, es decir, encontrando su diferencia.
Este tipo de razón la podemos escribir separando ambas cantidades por comparar con un signo menos (–). Así, la razón aritmética entre un par de números a y b, es: a – b, y se lee a es a b. El primer término de una razón aritmética se denomina antecedente, mientras que el segundo consecuente. antecedente consecuente
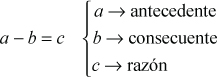
Actividad 1.13:
Un padre quiere repartir unos ahorros a sus dos hijos, pero al fin del mes uno de ellos se portó mal, por lo cual lo castigará dándole S/. 6000 menos que a su hermano. Si dispone de S/. 20 000 para repartir ¿cuánto le corresponde a cada uno?
b. Razón Geométrica: cada vez que se habla de razón en realidad se quiere hacer referencia a una razón geométrica.
La razón geométrica entre dos cantidades a y b es la comparación por cociente entre ambas, es decir, la división entre ellas. Este tipo de razón la podemos representar de dos formas: a través de un signo de división (÷ o:) o expresada en forma fraccionaria. De ambas formas se lee a es a b. Al igual que la razón aritmética el primer término se denomina antecedente, y el segundo, consecuente.
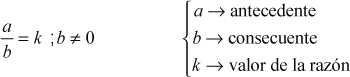
El tratamiento de las razones geométricas es similar al de las fracciones, es decir, se suman, restan, multiplican, dividen, simplifican y amplifican de la misma forma.
Ahora ¿a qué nos referimos específicamente cuando decimos 3 es a 5?, por ejemplo. La respuesta es muy sencilla: quiere decir que cada vez que tengamos 3 partes del antecedente tendremos 5 del consecuente, y en conjunto formamos 8 partes.
Actividad 1.14:
a. Al siguiente mes, el mismo padre (actividad anterior) tiene el mismo problema, uno de sus hijos se ha portado mal, por lo que quiere darle menos dinero que a su hermano, pero esta vez quiere que por cada S/. 3000 del hermano que se portó bien, el otro reciba solo S/. 2000, es decir quiere repartir el dinero a razón de 3 es a 2. Si dispone nuevamente de S/. 20 000, ¿cuánto dinero le corresponderá a cada uno?
b. Los ángulos de un triángulo están a razón de 1: 2 : 3 (recuerda que esto se lee; uno es a dos es a tres), sabiendo que la suma de los ángulos interiores de un triángulo es 180 grados ¿cuánto miden sus ángulos?
Proporciones
Una proporción es una igualdad entre dos razones equivalentes.
a. Proporción Aritmética o Equidiferencia: es la igualación de dos razones aritméticas equivalentes. A la diferencia entre las razones involucradas se la llama constante de proporcionalidad aritmética.
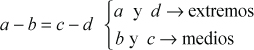
Propiedad fundamental:
«En toda proporción aritmética la suma de los extremos es igual a la suma de los medios»

Ejemplo:
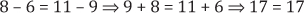
b. Proporción Geométrica o Equicocientes: una proporción geométrica (o simplemente proporción), es la igualación de dos razones geométricas equivalentes. En una proporción podemos distinguir sus partes por distintos nombres, están los extremos que son el antecedente de la primera razón y el consecuente de la segunda, y los medios, que son el consecuente de la primera razón y el antecedente de la segunda.
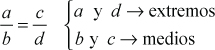
Propiedad fundamental:






