Un curso de álgebra

UN CURSO DE ÁLGEBRA

Educació. Materials 56

Gabriel Navarro

UN CURSO DE ÁLGEBRA

UNIVERSITAT DE VALÈNCIA

Colección: Educació. Materials

1.ª edición: abril 2002

2.ª edición, corregida y aumentada: mayo 2016

© Del texto: el autor, 2016

© De esta edición: Universitat de València, 2016

Coordinación editorial: Maite Simón

Maquetación: el autor

Corrección: Communico-Letras y Píxeles S.L.

Cubierta: Celso Hernández de la Figuera

ISBN: 978-84-9134-029-4

Para Isabel, Javier, Gabo y Nacho

Índice general

INTRODUCCIÓ

NOTA A LA SEGUNDA EDICIÓN

Capítulo 1. Conjuntos, aplicaciones, números

Capítulo 2. Grupos

Capítulo 3. Homomorfismos

Capítulo 4. Acciones de grupos

Capítulo 5. Grupos de permutaciones

Capítulo 6. Teoremas de Sylow

Capítulo 7. Anillos, polinomios y cuerpos

Capítol 8. Espacios vectoriales

Capítulo 9. Extensiones de cuerpos

Capítulo 10. Teoría de Galois

APÉNDICE: SOLUCIONES A ALGUNOS PROBLEMAS

BIBLIOGRAFÍA

ÍNDICE ANALÍTICO

Introducción

Este libro ofrece un primer curso de álgebra no lineal. En él, elegimos el objetivo de probar el gran teorema de Galois sobre la resolubilidad de ecuaciones polinómicas por radicales. Al mismo tiempo que aprendemos a «hacer» álgebra con el alumno, este tiene la sensación de que estamos resolviendo un problema natural con raíces históricas.

En la primera parte del libro introducimos los grupos.

Aunque tratamos de no apartarnos de nuestro objetivo, algunas veces no podemos resistir probar algunos teoremas que no son estrictamente necesarios para llegar a este. Por ejemplo, en el capítulo 5 damos una nueva demostración del teorema fundamental de los grupos abelianos finitos. Tampoco la teoría de Sylow sería esencial, aunque difícilmente un especialista en teoría de grupos finitos podrá dejar de presentarla.

La segunda parte del libro empieza en el capítulo 6 con los resultados más básicos sobre anillos y polinomios que nos permiten desarrollar la teoría de Galois. Seguramente, un especialista en teoría de anillos preferirá aumentar los contenidos de esta sección a costa de la parte de grupos.

En el capítulo 7, estudiamos las extensiones de cuerpos (donde por vez primera necesitaremos resultados elementales de álgebra lineal). Finalmente, en el capítulo 8, estamos ya preparados para estudiar la teoría de Galois. Por simplicidad, sus teoremas principales los probaremos sobre cuerpos de característica cero. (Una vez entendido este caso, el alumno interesado no tendrá dificultad en entender la teoría de Galois sobre cuerpos de cualquier característica).

Dependiendo del tiempo que quedara de curso, se podrían introducir algunos de los tópicos que no incluimos como construcciones con regla y compás o extensiones ciclotómicas.

A lo largo de los distintos capítulos, proponemos diversos ejercicios que solemos utilizar en las demostraciones. La resolución de estos siempre es rutinaria y permite al alumno practicar las definiciones y entender mejor los teoremas. Al final de cada capítulo, proponemos una serie de problemas (algunas de cuyas soluciones las encontrará el lector al final del libro).

En la bibliografía, damos la referencia de algunos de los textos con los que el alumno podrá continuar estudiando álgebra.

Finalmente, este libro no hubiera sido el mismo sin la colaboración de una profesora extraordinaria de álgebra: María Jesús Iranzo. También quiero dar las gracias a Alexander Moretó y a Francisco Pérez Monasor.

Valencia, febrero de 2002

Nota a la segunda edición

Han pasado catorce años desde que apareció la primera edición de este libro y el álgebra que aquí se explica no ha cambiado en este tiempo. Pero el autor sí, y quizá también el tipo de alumnos que llega a las facultades de matemáticas. Pienso por ejemplo en mi hijo Nacho, actualmente uno de esos estudiantes. Al recomendarle mi libro, estaba convencido de que iba a apreciar, entre otras cosas, la brevedad de alguna de mis demostraciones, pero no ha sido exactamente así (aunque tampoco, creo, al contrario).

De la experiencia de explicar el contenido de este libro a mis alumnos he aprendido mucho: cuándo y cómo explicar mejor un argumento, dónde introducir exactamente determinada definición, qué conceptos es necesario que se repasen de clase en clase, etc. Desafortunadamente, el estilo del aula no se puede trasladar literalmente a un libro. Aunque algo sí.

Aparte de corregir algún error, de mejorar demostraciones, añadir nuevos teoremas, reordenar ciertas secciones, o de escribir más ejemplos y problemas, he creído conveniente escribir dos capítulos nuevos. En el primero introduzco informalmente números, conjuntos y aplicaciones, tal y como lo hago en clase. Esta introducción no pretende ser exhaustiva. También, antes de empezar la teoría de Galois, he escrito un capítulo sobre espacios vectoriales, solo con los resultados básicos que luego necesitaré. (Por tanto, la numeración de los capítulos es distinta respecto de la pasada edición). Dependiendo de los objetivos específicos que se tengan en el curso o del nivel de los estudiantes, tanto estos nuevos capítulos como otros pueden ser omitidos.

Después de estos catorce años, no estoy seguro de ser mejor matemático; pero creo que he mejorado como profesor, y he procurado que esto quede reflejado en lo que he escrito.

Es posible que no haya una tercera edición del libro, por lo que he intentado que esta sea la definitiva. Quiero dar las gracias a Noelia Rizo, Lucía Sanus, Joan Tent y Carolina Vallejo por toda la ayuda prestada.

Valencia, abril de 2016

1. Conjuntos, aplicaciones, números

1

En este libro, un conjunto A es una colección de objetos a los que llamamos elementos de A. Dado un objeto x y un conjunto A, decimos que x pertenece a A si x es un elemento de A. En este caso escribimos x ∈ A. En caso contrario, decimos que x no pertenece a A, y escribimos x ∉ A.

Denotamos los conjuntos con letras mayúsculas, y los definimos especificando o describiendo con exactitud los elementos que pertenecen a ellos. Por ejemplo, A = {1, 2, 3, 4} es el conjunto cuyos elementos son 1, 2, 3 y 4. Así, escribimos 3 ∈ A y 5 ∉ A. El conjunto B = {1, {1, 2}, {1, 2, 3}} tiene tres elementos: 1, el conjunto {1, 2}, y el conjunto {1, 2, 3}. Por tanto, escribimos {1, 2, 3} ∈ B. El conjunto vacío ∅ es el conjunto que no tiene elementos. Un conjunto A es finito si tiene un número finito de elementos. En este caso escribimos |A| para denotar el número de elementos del conjunto A. Por ejemplo, |{1, 2, 3, 4}| = 4, |{1, {1, 2}, {1, 2, 3}}| = 3 y |∅| = 0.

No siempre es posible o conveniente listar todos y cada uno de los elementos de un conjunto: nos basta con que describamos con precisión los que pertenecen a él. Por ejemplo, el conjunto

C = {x ∈ ℕ | x = 2n + 1 para algún n ∈ ℕ}

es el conjunto de los números naturales impares. En este libro, los números naturales son los elementos del conjunto ℕ = {0, 1, 2, 3, …}. Algunos autores no consideran 0 como número natural, pero esta es una polémica inútil. La línea vertical “|” en la definición del conjunto C se lee “tal que”; así, decimos que C es el conjunto de los números naturales x tales que pueden escribirse de la forma x = 2n + 1 para algún n ∈ ℕ. Algunos autores utilizan “:” en lugar de la línea vertical. Los lectores deben ser conscientes de que diferentes autores pueden utilizar notaciones distintas y de que esto no es necesariamente negativo. Volviendo a C, podríamos haber escrito

C = {2n + 1 | n ∈ ℕ}

que es una notación más ágil.

Considaremos ahora el conjunto D = {n ∈ ℕ | 0 < n > 5} y lo comparamos con el conjunto A = {1, 2, 3, 4} definido en el segundo párrafo. Desde luego, observamos que D y A son iguales, pero necesitamos formular esto de forma precisa. Si A y B son conjuntos, decimos que A está contenido en B si para todo a ∈ A se tiene que a ∈ B. En este caso, escribimos A ⊆ B, y decimos que A es un subconjunto de B. En caso contrario, decimos que A no está contenido en B, y lo escribimos A ⊈ B. Los conjuntos A y B son iguales si A ⊆ B y B ⊆ A, y lo escribimos A = B. En caso contrario, escribimos A ≠ B. Observamos que ∅ ⊆ A para todo conjunto A.

En este punto, debemos sincerarnos con el lector para advertirle que esta aproximación náıf a la teoría de conjuntos tiene algunas consecuencias no deseadas, como la famosa paradoja de Russell. Es evidente que el conjunto de los números naturales no es un número natural, por lo que la expresión ℕ ∉ ℕ, aunque chocante, es cierta. Uno podría construir el conjunto X = {A | A es conjunto y A ∉ A}, y preguntarse si el propio X ∈ X o si X ∉ X. Por ejemplo, ℕ ∈ X pues ℕ ∉ ℕ. Sin embargo, si X ∈ X, esto significaría por definición que X ∉ X, y al contrario. Hemos llegado a una contradicción, pues no puede pasar algo y lo opuesto al mismo tiempo. En definitiva, parece claro que tenemos un problema con nuestra definición de conjunto.

La teoría de conjuntos puede ser desarrollada de una forma axiomática que evita este tipo de contradicciones, pero este libro no es el lugar adecuado para hacerlo. La lógica es la disciplina que se ocupa de este y de otros temas.

Por otra parte, no debemos preocuparnos en exceso, al menos en lo que aqúı se refiere. Es un hecho que la mayor parte de los matemáticos puede desarrollar una carrera exitosa utilizando nuestra definición de conjuntos sin contratiempo alguno en su vida (matemática). Digamos de una forma informal que mientras tratemos con conjuntos pequeños (el conjunto de todos los conjuntos definitivamente no es un conjunto pequeño), no nos vamos a encontrar con grandes problemas.

Dados dos conjuntos A y B, podemos construir nuevos conjuntos. Por ejemplo, la unión de A y B es el conjunto

A ∪ B = {x | x ∈ A ó x ∈ B}.

La intersección es el conjunto

A ∩ B = {x | x ∈ A y x ∈ B}.

La diferencia de A y B es

A − B = {x | x ∈ A y x ∉ B}.

El producto cartesiano de A y B es el conjunto de pares

A × B = {(a, b) | a ∈ A, b ∈ B},

donde entendemos que (a, b) = (a′, b′) si y solo si a = a′ y b = b′.

Si A = {1, 2, 3} y B = {3, 4}, entonces A ∪ B = {1, 2, 3, 4}, A ∩ B = {3}, A − B = {1, 2} y A × B = {(1, 3), (1, 4), (2, 3), (2, 4), (3, 3), (3, 4)}.

Desde luego, podemos unir o intersectar una colección arbitraria de conjuntos. Si I es un conjunto, y para cada i ∈ I tenemos definido un conjunto Ai, que depende de i, entonces definimos

Por ejemplo, si para n ∈ ℕ, definimos An = {m ∈ ℕ | m ≥ n}, entonces tenemos que

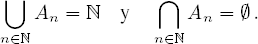
Si A1, …, An son conjuntos, definimos

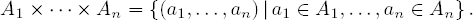
Si el lector está leyendo este primer capítulo, cabe la posibilidad de que no esté demasiado habituado a probar teoremas, habilidad que solo se adquiere con práctica, y leyendo muchas demostraciones. Probamos nuestro primer teorema.

Teorema 1.1 (Leyes de Morgan) Supongamos que X, I y Ai para i ∈ I son conjuntos. Entonces

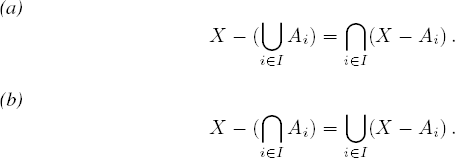
Demostración. Probamos (a), por ejemplo. Queremos probar que dos conjuntos son iguales. Por tanto, debemos probar que X − (⋃i∈I Ai) está contenido en ⋂i∈I (X − Ai), y la inclusión contraria. Sea x ∈ X − (⋃i∈I Ai). Esto significa que x ∈ X y que x ∉ ⋃i∈I Ai. Por la definición de unión de una colección de conjuntos, tenemos que x ∉ Ai para todo i ∈ I. Así, x ∈ X − Ai para todo i ∈ I, y por la definición de intersección de una colección de conjuntos, concluimos que x ∈ ⋂i∈I (X − Ai). Recíprocamente, si x ∈ ⋂i∈I (X − Ai), tenemos que x ∈ X y x ∉ Ai para todo i. Entonces x ∈ X y x ∉ ⋃i∈I Ai, y por tanto x ∈ X − (⋃i∈I Ai).

2

Los conjuntos se relacionan mediante aplicaciones. Si A y B son conjuntos, una aplicación o función de A en B, que escribimos

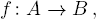
es una correspondencia (regla o criterio) que asigna a cada elemento a ∈ A un único elemento f(a) de B. A f(a) se le llama la imagen de a mediante f. El conjunto A se llama el dominio o conjunto inicial de f. El conjunto B se llama el codominio o conjunto final de f. El conjunto imagen

f(A) = {f(a) | a ∈ A}

es el subconjunto de B formado por todas las imágenes mediante f de los elementos de A.

Podemos imaginar una función como una máquina cuyos inputs son los elementos de A. Damos a ∈ A a la máquina y esta produce un output perfectamente determinado que es f(a) ∈ B. Para el lector riguroso que no esté satisfecho ni con la definición ni con la idea de la máquina, podemos definir una función f : A → B como un subconjunto X ⊆ A × B tal que X ∩ ({a} × B) tiene exactamente un elemento para todo a ∈ A; pero esto es innecesariamente complicado. Si pensamos un momento sobre esta última definición, observamos que X es el grafo de la función f.

El lector está seguramente acostumbrado a tratar con funciones entre números reales como las aplicaciones f : ℝ → ℝ dada por f(x) = x2 + 1, o g : ℝ → ℝ dada por g(x) = sen(x). O incluso con funciones h : ℝ × ℝ → ℝ definidas por

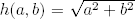
Ejercicio 1.1 Sean A y B conjuntos. Sea BA el conjunto de las aplicaciones de A en B. Si A tiene n elementos y B tiene m elementos, probar que BA tiene mn elementos.

Dos funciones f : A → B, g : C → D son iguales si A = C, B = D y f(a) = g(a) para todo a ∈ A. Por ejemplo, las funciones f : ℤ → ℤ y g : ℤ → ℕ dadas por f(z) = g(z) = z2 no son iguales porque sus conjuntos finales son distintos.

Para todo conjunto A, tenemos definida la función identidad 1A : A → A con 1A(a) = a para todo a ∈ A.

Con frecuencia, lo primero que nos preguntamos sobre una aplicación f es si es inyectiva o suprayectiva; estos dos adjetivos se asocian de forma natural a las funciones. Una aplicación f : A → B es inyectiva si f(a1) = f(a2) solo si a1 = a2, para a1, a2 ∈ A. En otras palabras, f es inyectiva si elementos distintos de A tienen imágenes distintas en B. Si queremos comprobar que una función f es inyectiva, escribimos la igualdad f(a1) = f(a2) y tratamos de averiguar si a1 es necesariamente igual a a2 o no. Informalmente, si f es una aplicación inyectiva, pensamos que B contiene un subconjunto (f(A)) que tiene las mismas propiedades que A.

Ejercicio 1.2 Si A tiene n elementos, B tiene m elementos, y f : A → B es injectiva, probar que n ≤ m.

Una aplicación f : A → B es suprayectiva si f(A) = B. En otras palabras, si para todo b ∈ B existe a ∈ A tal que f(a) = b. Si queremos comprobar si una función f es suprayectiva, elegimos un elemento b ∈ B arbitrario y lo intentamos expresar como f(a) para algún a de A.

Ejercicio 1.3 Si A tiene n elementos, B tiene m elementos, y f : A → B es suprayectiva, probar que n ≥ m.

Teorema 1.2 Supongamos que A y B tienen n elementos, y sea f : A → B. Entonces f es inyectiva si y solo si f es suprayectiva.

Demostración. Esta es la primera vez en este libro que probamos un teorema si y solo si, por lo que hacemos una pausa para explicar lo que significa. Cuando tengamos que probar que un enunciado P es verdadero si y solo si un enunciado Q es verdadero, tenemos que probar que P implica Q (esto es, suponiendo P demostramos Q) y que Q implica P (suponiendo Q demostramos P).

Escribamos A = {a1, …, an}. Así, f(A) = {f(a1), …, f(an)} ⊆ B.

Supongamos que f es inyectiva. Entonces f(A) tiene n elementos, pues f(ai) ≠ f(aj) si i ≠ j. Como B tiene n elementos, necesariamente f(A) = B, y por tanto f es suprayectiva. Recíprocamente, si f es suprayectiva entonces f(A) = B tiene n elementos, y por tanto no puede ocurrir que f(ai) = f(aj) para distintos i y j.

Finalmente, una aplicación f : A → B es biyectiva si f es inyectiva y suprayectiva. Las aplicaciones biyectivas (o biyecciones) son las mejores aplicaciones que podemos encontrar entre dos conjuntos.

Ejemplo 1.1 La función f : ℕ → ℕ dada por f(n) = 2n + 1 es inyectiva, pues si f(n) = f(m), entonces 2n + 1 = 2m + 1, y concluimos que n = m. Sin embargo, f no es suprayectiva, pues no podemos hallar ningún n ∈ ℕ tal que f(n) = 2. La función g : {1, 2, 3} → {a, b} dada por g(1) = a, g(2) = b y g(3) = a no es inyectiva, pues g(1) = g(3). Sin embargo, g es suprayectiva.

Sean ahora f : ℝ → ℝ y g : ℝ → ℝ definidas por f(x) = sen(x) y g(x) = x2. Observamos primero que g no es inyectiva pues g(−1) = g(1). Sin embargo, si definimos h : ℝ+ → ℝ con h(x) = x2, donde ℝ+ = {x ∈ ℝ | x ≥ 0}, entonces h es ahora inyectiva (pero no suprayectiva pues −1 no está en la imagen de h). Finalmente, si definimos t : ℝ+ → ℝ+ con t(x) = x2, entonces t es biyectiva. Algo semejante ocurre con f(x) = sen(x). La función s : [−π/2, π/2] → [−1, 1] dada por s(x) = sen(x) puede comprobarse que es una biyección.