Un curso de álgebra

¿Por qué es tan importante tener aplicaciones biyectivas? Esencialmente por dos razones. La primera es que una función biyectiva posee una función inversa. En el ejemplo anterior, la inversa de s es la función arcsen : [−1, 1] → [−π/2, π/2], mientras que la inversa de t es la función ráız cuadrada. La segunda razón es que si existe una función biyectiva entre A y B cualquier propiedad que satisfaga A desde el punto de vista de la teoría de conjuntos la va a satisfacer B, y recíprocamente. Es decir, que desde la perspectiva de conjuntos, A y B son equivalentes. Esto nos permitirá después, por ejemplo, comparar conjuntos y sus tamaños.

Si f : A → B y g : B → C, podemos crear una nueva función

g ∘ f : A → C

definida por

(g ∘ f)(a) = g(f(a))

que se llama la composición de g y f.

Por ejemplo, si f : ℝ → ℝ es la función f(x) = x2 + 1 y g(x) = sen(x), entonces (g ∘ f)(x) = sen(x2 + 1) y (f ∘ g)(x) = sen(x)2 + 1.

La primera parte del siguiente ejercicio nos dice que la composición de aplicaciones es asociativa.

Ejercicio 1.4 (i) Si f : A → B, g : B → C y h : C → D son aplicaciones, probar que

(h ∘ g) ∘ f = h ∘ (g ∘ f).

(ii) Si f : A → B es un aplicación, probar que f ∘ 1A = f y 1B ∘ f = f.

Lema 1.3 Sean f : A → B y g : B → C aplicaciones.

(a) Si f y g son inyectivas, entonces g ∘ f es inyectiva.

(b) Si f y g son suprayectivas, entonces g ∘ f es suprayectiva.

(c) Si g ∘ f es inyectiva, entonces f es inyectiva.

(d) Si g ∘ f es suprayectiva, entonces g es suprayectiva.

Demostración. (a) Si g(f(a1)) = g(f(a2)), deducimos que f(a1) = f(a2) por ser g inyectiva. Por ser f inyectiva, tenemos que a1 = a2.

(b) Si c ∈ C, entonces existe b ∈ B tal que g(b) = c, por ser g suprayectiva. Por ser f suprayectiva, existe a ∈ A tal que f(a) = b. Entonces g(f(a)) = c.

(c) Si f(a1) = f(a2), entonces g(f(a1)) = g(f(a2)). Como g ∘ f es inyectiva, deducimos que a1 = a2.

(d) Si c ∈ C, por hipótesis existe a ∈ A tal que g(f(a)) = c. Si b = f(a), deducimos que g(b) = c

Decimos que una función f: A → B es invertible si existe g: B → A tal que f ∘ g = 1B y g ∘ f = 1A. Observamos que la función g, si existe, es única. Efectivamente, si h: B → A también satisface h ∘ f = 1A, entonces

h = h ∘ 1B = h ∘ (f ∘ g) = (h ∘ f) ∘ g = 1A ∘ g = g.

La función g se llama la función inversa de f y se escribe g = f−1. Observamos que en este caso f−1 es también invertible y que (f−1)−1 = f.

Teorema 1.4 Sea f : A → B. Entonces f es invertible si y solo si f es biyectiva.

Demostración. Supongamos que f es biyectiva. Construimos g : B → A de la siguiente manera. Dado b, sabemos que existe a ∈ A tal que f(a) = b, pues f es suprayectiva. Como f es inyectiva, a es único, y por tanto b unívocamente determina a. Definimos g(b) = a. Es inmediato que f ∘ g = 1B y g ∘ f = 1A. Recíprocamente, supongamos que f es invertible y sea f−1 : B → A su inversa. Como f ∘ f −1 = 1B y f −1 ∘ f = 1A son biyectivas, el teorema se sigue por el lema 1.3 partes (c) y (d).

3

Si A es un conjunto, una relación en A es un subconjunto

R ⊆ A × A.

Decimos que a está relacionado con b si (a, b) ∈ R. Podemos pensar que una relación es sencillamente una función f : A × A → {sí, no}, donde R = {(a, b) ∈ A × A | f(a, b) = sí}.

Por ejemplo, en el conjunto A = {1, 2, 3}, definimos la relación

R = {(1, 1), (1, 2), (3, 2)}.

En este caso, 1 está relacionado con 1 y con 2, 2 no está relacionado con ningún elemento, y 3 está relacionado con 2. Muchas veces, en lugar de especificar R, es más sencillo describir cuándo dos elementos están relacionados. Por ejemplo, en el conjunto A de los habitantes de una ciudad, podemos decir que dos elementos de A están relacionados si viven en el mismo edificio. En este caso, observamos que cualquier a ∈ A está relacionado consigo mismo, entre otras propiedades que analizamos a continuación. Necesitamos cierto lenguaje para hablar de relaciones.

Definición 1.5 Sea A un conjunto y R ⊆ A × A una relación en A.

(a) Decimos que R es reflexiva si (a, a) ∈ R para todo a ∈ A.

(b) Decimos que R es simétrica si siempre que (a, b) ∈ R, entonces (b, a) ∈ R.

(c) Decimos que R es antisimétrica si siempre que (a, b) ∈ R y (b, a) ∈ R, entonces a = b.

(d) Decimos que R es transitiva si siempre que (a, b), (b, c) ∈ R, entonces (a, c) ∈ R.

Muy pocas relaciones en un conjunto A son interesantes. De hecho, las relaciones interesantes son esencialmente de dos tipos. Una relación R es de equivalencia si R es reflexiva, simétrica y transitiva. Una relación R es una relación de orden si R es reflexiva, antisimétrica y transitiva.

Ejemplo 1.2

(a) En el conjunto ℝ de los números reales, definimos la relación (a, b) ∈ R si y solo si a ≤ b. Esta es una relación de orden.

(b) En el conjunto de habitantes de una ciudad, vivir en el mismo edificio establece una relación de equivalencia.

(c) En el plano ℝ2, decimos que (x1, y1) está relacionado con (x2, y2) si se tiene que

Esto define en el plano una relación de equivalencia.

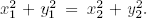
(d) Si f : A → B es una aplicación, definimos R = {(a1, a2) | f(a1) = f(a2)}. Entonces R es una relación de equivalencia.

(e) Si A es un conjunto, definimos una relación en el conjunto P (A) de todos los subconjuntos de A. Decimos que X e Y están relacionados si X ⊆ Y. Esto define una relación de orden en P (A).

Siempre que tengamos una relación de equivalencia R sobre un conjunto A, dicho conjunto queda partido en trozos disjuntos. (Dos conjuntos A y B son disjuntos si A ∩ B = ∅). Este es un hecho relevante. En el ejemplo 1.2 (b), los habitantes quedan distribuidos en edificios; en el ejemplo 1.2 (c), los elementos del plano quedan distribuidos en círculos de radio r para r ≥ 0. En general, cada elemento a ∈ A vive en su clase de equivalencia.

Una partición de un conjunto A es un conjunto P de subconjuntos no vacíos de A tales que

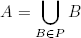
y B ∩ C = ∅ para todos B, C ∈ P distintos.

Si A es un conjunto con una relación de equivalencia R, para cada a ∈ A se define [a] = {b ∈ A | (a, b) ∈ R}, que se llama la clase de equivalencia de a. Observamos que a ∈ [a] ⊆ A.

Teorema 1.6 Sea A un conjunto con R una relación de equivalencia, y sea P = {[a] | a ∈ A} el conjunto de clases de equivalencia de A. Entonces P es una partición de A.

Demostración. Como a ∈ [a], está claro que [a] ≠ ∅ y que

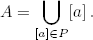
Si c ∈ [a], probamos a continuación que [c] = [a]. Sea x ∈ [c]. Entonces (x, c) ∈ R. Como (c, a) ∈ R, tenemos que (x, a) ∈ R y x ∈ [a]. Recíprocamente, si x ∈ [a], entonces (x, a) ∈ R. Como (a, c) ∈ R, tenemos que (x, c) ∈ R y x ∈ [c], como queríamos. Finalmente, supongamos que [a] ∩ [b] ≠ ∅, y sea c ∈ [a] ∩ [b]. Por lo anterior, tenemos que [a] = [c] = [b].

4

¿Todos los conjuntos infinitos tienen el mismo número de elementos? ¿Hay algún conjunto infinito con menos elementos que ℕ? ¿Cómo comparamos infinitos?

Al principio, puede que la intuición no nos sea del todo útil. Es famoso el Hotel de Hilbert que tiene un número infinito de habitaciones numeradas {1, 2, 3, …}, todas ellas ocupadas.

Al llegar un huésped nuevo, el conserje del hotel, lejos de rechazarlo, traslada al ocupante de la habitación n a la n+1, y deja así la primera habitación libre para el huésped nuevo. Este conserje ni se inmuta cuando momentos después ve aparecer llegando a su hotel un autobús con infinitos turistas {1, 2, 3, …}: traslada al ocupante de la habitación n a la habitación 2n y al turista m a la habitación 2m − 1. Tampoco se preocupa el conserje cuando esta vez aparece un número infinito de autobuses {a1, a2, …, ak, …} cada uno de ellos cargado de infinitos turistas {ak1, ak2, …}… pero vamos a dejarlo aquí.

Para comparar infinitos, las funciones biyectivas son fundamentales. Si existe f : A → B biyectiva, decimos que A y B tienen el mismo cardinal (o son equipotentes), y lo escribimos |A| = |B|. En caso contrario, escribimos |A| ≠ |B|.

Teorema 1.7 Sean A, B y C conjuntos.

(a) |A| = |A|.

(b) Si |A| = |B|, entonces |B| = |A|.

(c) Si |A| = |B| y |B| = |C|, entonces |A| = |C|.

Demostración. Para probar (a), utilizamos la función identidad 1A. Si existe una función biyectiva f : A → B, entonces f−1 es biyectiva, y (b) queda probado. Para probar (c), usamos que la composición de funciones biyectivas es biyectiva por el lema 1.3.

El lector debe ser consciente de que en el teorema anterior, no hemos escrito que tener el mismo cardinal establece una relación de equivalencia pues a continuación estaríamos obligados a añadir “en el conjunto de todos los conjuntos”, y como ya hemos dicho antes, no debemos tratar con conjuntos demasiado grandes. Al principio de este capítulo, habíamos definido |A| para un conjunto finito A, como el número de elementos de A. Los ejercicios 1.2 y 1.3 nos aseguran que la notación |A| = |B| es consistente.

Asociado a un conjunto A hay otro conjunto especial que hemos utilizado en el ejemplo 1.2 (e):

P (A) = {B | B ⊆ A}

que se llama el conjunto potencia de A (o partes de A). Lo más importante de P (A) es que tiene más elementos que A.

Teorema 1.8 Sea A un conjunto.

(a) La aplicación f : A → P (A) dada por f(a) = {a} es inyectiva.

(b) No existe ninguna aplicación g : A → P (A) suprayectiva.

Demostración. La primera parte es trivial. Sea ahora g : A → P (A) suprayectiva. Sea B = {a ∈ A | a ∉ g(a)} ⊆ A. Como g es suprayectiva, entonces existe a ∈ A tal que g(a) = B. Si a ∈ B, entonces a ∉ g(a) = B, lo cual no es posible. Si a ∉ B, entonces a ∈ g(a), y por tanto a ∈ B, lo cual tampoco es posible.

Según el teorema 1.8, P (ℕ) tiene más elementos que ℕ, y de hecho se puede probar que |P (ℕ)| = |ℝ|. No nos podemos resistir a mencionar la llamada hipótesis del continuo, establecida por George Cantor en 1878. Si A y B son conjuntos, escribimos |A| ≤ |B| si existe f : A → B inyectiva, y |A| < |B| si |A| ≤ |B| y |A| ≠ |B|. Por ejemplo, acabamos de probar que |A| < |P (A)| para todo conjunto A. La hipótesis del continuo, que constituye el primer problema de la famosa lista de problemas propuestos por Hilbert, afirma que no existe ningún conjunto A tal que |ℕ| < |A| < |ℝ|. En 1963 Paul Cohen probó que este enunciado es indemostrable. Este es otro concepto que no cabe en el presente libro. El autor sinceramente espera no haber interesado demasiado al lector en lógica para que renuncie al álgebra.

La siguiente propiedad de ℕ es fundamental: nos dice que en ℕ existe un buen orden.

Teorema 1.9 (teorema del buen orden en ℕ) Si A es un subconjunto no vacío de ℕ entonces existe a ∈ A tal que a ≤ b para todo b ∈ A. Este elemento a es único.

Demostración. Primero probamos la existencia de a. Como A no es vacío, sea a1 ∈ A. Si a1 ≤ b para todo b ∈ A, ya tendríamos el elemento que buscamos. En caso contrario, existe a2 ∈ A tal que a2 < a1. Si a2 ≤ b para todo b ∈ A, de nuevo lo tendríamos. Como entre 0 y a1 hay solo un número finito de elementos, este proceso no se puede repetir un número infinito de veces. Así, podemos llegar a encontrar a ∈ A tal que a ≤ b para todo b ∈ A.

A continuación probamos la unicidad de a. En efecto, si existiera otro elemento c ∈ A con la misma propiedad, tendríamos que a ≤ c y c ≤ a, con lo que a = c.

Al elemento a en el teorema 1.9 se le llama el menor elemento de A, y lo denotamos por min(A).

Decimos que un conjunto A es numerable si |ℕ×| = |A|, donde ℕ× = {1, 2, 3, …}. Algunos autores incluyen los conjuntos finitos entre los conjuntos numerables. Vemos que si A es numerable, entonces existe una aplicación biyectiva f : ℕ× → A, y así podemos escribir

A = {f(1), f(2), f(3), …}.

En definitiva, si A es numerable, entonces los elementos de A se pueden enumerar.

Teorema 1.10 Supongamos que A es un subconjunto infinito de ℕ. Entonces A es numerable.

Demostración. Como A no es vacío, sea a1 = min(A). Como A − {a1} no es vacío, sea a2 = min(A − {a1}). En general, si tenemos definidos a1, …, ak, como A − {a1, …, ak} no es un conjunto vacío (pues A es infinito), podemos definir

ak+1 = min(A − {a1, …, ak})

para k ≥ 0. Observamos pues que tenemos definidos

a1 < a2 < … < ak < ak+1 < …

una cadena de elementos de A. Definimos f : ℕ× → A con f(k) = ak. Como an < am si n < m, observamos que f es inyectiva.

Probamos finalmente que f es suprayectiva. Sea a ∈ A. Sea B = {n ∈ A | n < a}. Si B = ∅, entonces a = a1 = f(1). En otro caso, B es un conjunto finito no vacío, que por tanto se puede escribir B = {a1, …, at} para algún t. Entonces a = at+1 = f(t + 1), y el teorema queda probado.

Corolario 1.11 Si A es numerable y B ⊆ A, entonces B es finito o numerable.

Demostración. Supongamos que B es infinito. Sea f : A → ℕ× una aplicación biyectiva. Aplicamos el teorema 1.10 al conjunto infinito f(B).

En los problemas guiaremos al lector sobre cómo probar que el conjunto de los números racionales es numerable, o que el de los números reales no lo es, entre otras propiedades.

5

El conjunto de los números enteros es

ℤ = {…, −n, …, −3, −2, −1, 0, 1, 2, 3, …, n, … | n ∈ ℕ}.

Suponemos que el lector está familiarizado con la suma y la multiplicación de números enteros. Es decir, en ℤ podemos sumar y multiplicar elementos: 2 + 3 = 5 o (−3)3 = −9. (Más adelante, diremos que ℤ con estas operaciones es un anillo). También utilizamos que ℤ es un conjunto con un orden: 3 > 0, −5 ≤ 5 o 2 ≤ 2.

Estamos acostumbrados a dividir dos números enteros n y m, y obtener un dividendo d y un resto r. Este es el llamado algoritmo de división.

Teorema 1.12 (algoritmo de división) Sean n ∈ ℤ y 0 < m ∈ ℕ. Entonces existen dos únicos enteros d y r tales que n = dm + r con 0 ≤ r < m.

Demostración. Consideremos el conjunto A = {n−dm | d ∈ ℤ y n−dm ≥ 0}. Es decir, A está formado por los números naturales de la forma n − dm, con d ∈ ℤ. Si n ≥ 0, entonces n − (−n)m = n(1 + m) ≥ 0, y deducimos que n(1 + m) ∈ A. Si n ≤ 0, entonces n − nm = n(1 − m) ≥ 0, y deducimos que n − nm ∈ A. En cualquier caso, concluimos que A ≠ ∅. Por el teorema 1.9, sea r el menor elemento de A. Como r ∈ A, entonces existe d ∈ ℤ tal que n − dm = r. Por tanto, n = dm + r. Si r ≥ m, tendríamos que

0 ≤ r − m = (n − dm) − m = n − (d + 1)m ∈ A.

Pero r es el menor elemento de A y r − m < r. Esta contradicción prueba que r < m. Por tanto, hemos hallado d y r tales que n = dm + r con r < m.

Supongamos finalmente que d1 y 0 ≤ r1 < m también satisfacen que n = d1m + r1. Supongamos que r1 ≥ r, por ejemplo. Como n = dm + r = d1m + r1, tendremos que 0 ≤ r1 − r = (d − d1)m ≤ r1 < m. Necesariamente, d − d1 = 0 y por tanto r1 = r.

Vemos que el algoritmo de división es una consecuencia del teorema del buen orden en ℕ. Otra consecuencia de este es el llamado principio de inducción. En la práctica funciona así: Queremos probar que a partir de un cierto número natural k (habitualmente el 0 o el 1), todos los naturales mayores o iguales que k satisfacen una cierta propiedad. La estrategia que seguimos es la siguiente: primero probamos que k satisface la propiedad; y después probamos que si n ≥ k la satisface, entonces n + 1 también la satisface. El principio de inducción garantiza, entonces, que cualquier n ≥ k satisface la propiedad. En efecto, sea A el conjunto de números naturales mayores o iguales que k que satisfacen la propiedad, y sea B = {n ∈ ℕ | n ≥ k}. Queremos probar que A = B. Como A ⊆ B, en caso contrario tendríamos que