Un curso de álgebra

∅ ≠ B − A = {b ∈ B | b ∉ A} ⊆ ℕ.

Por el teorema del buen orden en ℕ, sea n el menor elemento de B − A. Notar que n > k, pues k ∈ A (ya que k satisface la propiedad). Entonces n − 1 no está en B − A, pues n es el menor elemento de B − A. Así, n − 1 ≥ k satisface la propiedad y por hipótesis también la satisface

n = (n − 1) + 1.

Esta es la contradicción final.

Ejemplo 1.3 Probamos que

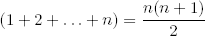
por inducción. Primero comprobamos que la igualdad es cierta para n = 1. Después suponemos que es cierta para n y la probamos para n + 1. Tenemos que

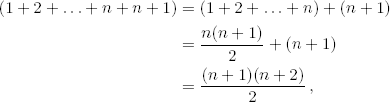
como queríamos probar.

El concepto fundamental en ℤ es la divisibilidad. Si a, b ∈ ℤ, con b ≠ 0, decimos que b divide a a si existe c ∈ ℤ tal que cb = a. A menudo se escribe b | a. En tal caso se dice que b es un divisor de a, y notamos que |c||b| = |a| (donde el valor absoluto |a| = a si a ≥ 0 y −a si a < 0). Si a ≠ 0, observamos que |b| ≤ |a|, por lo que concluimos que un entero a no cero solo tiene un número finito de divisores. Dados dos enteros n, m ∈ ℤ no cero, existe por tanto un mayor número natural 1 ≤ d que divide a ambos. Se dice que d es el máximo común divisor de n y m, y se escribe d = mcd(n, m). Si d = 1, entonces n y m se dice que son coprimos.

Ejercicio 1.5 Si a divide a b y a c, probar que a divide a b + c. Si a divide a b, entonces a divide a bz para todo z ∈ ℤ.

Teorema 1.13 (máximo comú divisor) Sean n, m ∈ ℤ no cero, y sea d = mcd(n, m).

(a) Entonces d es el menor elemento del conjunto

{un + vm | u, v ∈ ℤ, un + vm > 0}.

En particular, existen enteros u, v ∈ ℤ tales que d = un + vm.

(b) Si e divide a n y a m, entonces e divide a d.

Demostración. Consideramos el conjunto

A = {un + vm | u, v ∈ ℤ, un + vm > 0},

que claramente no es vacío. (Por ejemplo, si n > 0 y m < 0, n + m2 ∈ A). Sea f = un + vm el menor elemento de A. Por el algoritmo de división, n = qf + r con 0 ≤ r < f. Entonces,

r = n − qf = n − q(un + vm) = (1 − qu)n + (−vq)m.

Como r < f, esto solo puede ser cierto si r = 0. Deducimos que f divide a n y, análogamente, a m. En particular, f ≤ d, por definición de d. Como n = n1d, y m = m1d, tenemos que 0 < f = un1d + vm1d = (un1 + vm1)d ≥ d, y concluimos que d = f.

Para la parte (b), si e divide a n y a m, por el ejercicio 1.1, concluimos que e divide a un + vm = d.

Los números primos son fundamentales en matemáticas. Un número natural p > 1 es primo si no se puede escribir como p = ab, con a, b > 1. Es decir, si sus únicos divisores positivos son 1 y p. Observamos que si p es primo y n ∈ ℕ, entonces mcd(n, p) = 1 o p, pues mcd(n, p) es un divisor de p. Concluimos por tanto que o bien p divide a n o que p y n son coprimos.

Teorema 1.14 (Euclides) Sean n, m ∈ ℤ no cero.

(a) n y m son coprimos si y solo si existen u, v ∈ ℤ tales que un + vm = 1.

(b) Supongamos que n y m son coprimos. Si z ∈ ℤ, entonces n divide mz si y solo si n divide a z.

(c) Si p es primo, entonces p divide a nm si y solo si p divide a n o a m. En particular, si p divide a un producto de enteros n1 … nk, entonces p divide a algún ni.

Demostración. Si n y m son coprimos, ya sabemos que existen u, v ∈ ℤ tales que un + vm = 1, por el teorema 1.13 (a). Recíprocamente, si un + vm = 1, y d divide a n y a m, por el ejercicio 1.1, d divide a un + vm = 1, y esto completa el apartado (a).

En (b), supongamos que n divide a mz. Sabemos que 1 = un + vm para ciertos u, v ∈ ℤ, y que existe x ∈ ℤ tal que nx = mz. Ahora,

z = unz + vmz = unz + vnx = (uz + vx)n,

y deducimos que n divide a z. La otra implicación es obvia.

Para probar el apartado (c), si suponemos que p divide a nm y que p no divide a n, tenemos que mcd(p, n) = 1, y aplicamos el apartado (b). La segunda parte del apartado (c) se prueba fácilmente por inducción sobre k.

Teorema 1.15 (teorema fundamental de la aritmética) Si n > 1 es un entero, entonces n se escribe de forma única como

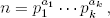
donde p1 < … < pk son primos, y a1, …, ak son números naturales no cero.

Demostración. Primero probamos la unicidad. Si

son dos expresiones como las del teorema, tenemos que p1 divide deducimos que p1 divide a cierto qi por el teorema 1.14 (c). Por tanto, p1 = qi, pues qi es primo. Por el mismo argumento, tenemos que q1 = pj para cierto j. Entonces qi = p1 ≤ pj = q1, por lo que deducimos que i = 1 y p1 = q1. Utilizamos el mismo argumento para n/p1.

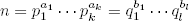
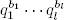
Para probar que cada n > 1 se escribe como producto de primos utilizamos inducción. Si n es primo, ya está. En caso, contrario, n = ab con a, b < n. Por inducción, a y b son producto de primos, y por tanto también lo es n.

El conjunto de números racionales es

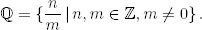
Suponemos que el lector está familiarizado con la suma y la multiplicación de números racionales, y sus propiedades más elementales. Por ejemplo,

si y solo si ad = bc,

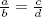
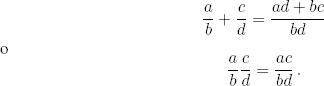
Es sencillo construir el conjunto de los números racionales a partir de los números enteros como clases de equivalencia. (En el problema 1.10, explicamos cómo hacer esta construcción).

En la segunda parte de este libro, cuando desarrollemos la teoría de Galois, trabajaremos con el conjunto de números reales ℝ y el de los complejos ℂ. La construcción rigurosa de ℝ es uno de los hitos de la matemática del siglo XIX, pero esta es materia de nuestros colegas los analistas. Apenas utilizaremos propiedades de los números reales, más que aquellas que están directamente asociadas a su suma, multiplicación (ℝ es un cuerpo) y a los polinomios. Por ejemplo, dado 0 ≤ a ∈ ℝ y 0 < n ∈ ℕ supondremos que existe un único número real 0 ≤ b ∈ ℝ tal que bn = a. Este número b se escribe

Un número real a ∈ ℝ es irracional si a ∉ ℚ. Como los ceros del polinomio xn − 1 son fundamentales en teoría de Galois, un poco de trigonometría también será necesaria.

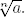
Recordamos que un entero n ∈ ℕ es un cuadrado si n = a2 para cierto a ∈ N.

Teorema 1.16 Sean n, m ∈ ℕ no cero con mcd(n, m) = 1. Entonces

si y solo si n y m son cuadrados.

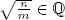
Demostración. Suponemos que

, y probamos que n y m son cuadrados. Por ejemplo, probamos que n es un cuadrado. Sea p un primo y supongamos que pf es la mayor potencia de p que divide a n con f ≥ 1. Es suficiente con probar que f es par y luego utilizar el teorema fundamental de la aritmética. Por hipótesis, podemos escribir

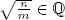
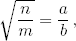
donde a, b ∈ ℕ. Entonces

b2n = a2m.

Como n y m son coprimos, sabemos que p no divide a m. Por tanto, si pe es la mayor potencia de p que divide a b, tenemos que

es la mayor potencia de p que divide a a2. Concluimos que 2e + f es par, y por tanto, también lo es f. Por el teorema fundamental de la aritmética, concluimos que n es un cuadrado. La implicación contraria es trivial.

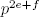
Como decimos, en la segunda parte del libro estaremos interesados en polinomios y en sus ráıces. Por ejemplo, ¿cuáles son los ceros del polinomio x8 − 1? Para contestar, necesitamos trabajar con números complejos y una cierta trigonometría.

El cuerpo de los nú meros complejos ℂ se define formalmente como el conjunto ℝ2 = {(a, b) | a, b ∈ ℝ} con la suma (a, b) + (c, d) = (a + c, b + d) y la multiplicación (a, b)(c, d) = (ac−bd, ad+bc). Si llamamos i = (0, 1), vemos que i2 = (−1, 0). Si identificamos a con (a, 0), podemos escribir (a, b) = a+bi, que es la notación que vamos a utilizar. Así, por ejemplo, tenemos que ℝ ⊆ ℂ o que

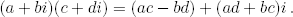
Teorema 1.17 (fórmula de De Moivre) Si a ∈ ℝ y n ∈ ℕ, entonces

(cos(a) + sen(a)i)n = cos(na) + sen(na)i.

Demostración. Si suponemos las igualdades trigonométricas

cos(α + β) = cos(α)cos(β) − sen(α)sen(β)

y

sen(α + β) = sen(α)cos(β) + cos(α)sen(β),

la fórmula de De Moivre es inmediata por inducción sobre n.

Con la fórmula de De Moivre, ya podemos calcular los ceros del polinomio xn − 1: son los n números complejos ξk, donde

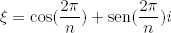
y 0 ≤ k ≤ n−1. Estos n números complejos son muy importantes y se denominan las ráıces n-ésimas de la unidad. Los podemos situar en la circunferencia de radio 1 al dividirla en n-ángulos iguales. Por ejemplo, las ráıces 4-ésimas de la unidad son {1, i, −1, −i}.

PROBLEMAS

1. Sean A, B, C conjuntos. Probar:

(i) Si A ∩ B = A ∩ C y A ∪ B = A ∪ C, entonces B = C.

(ii) (A − B) ∪ (B − A) = (A ∪ B) − (A ∩ B).

(iii) A ∩ (B − C) = (A ∩ B) − (A ∩ C).

(iv) A − (A − B) = A ∩ B.

(v) (B ∪ C) − A = (B − A) ∪ (C − A).

(vi) (A − B) − C = (A − B) ∩ (A − C).

2. Sea f : X → Y una aplicación. Si A ⊆ X, se define f(A) = {f(a) | a ∈ A}. Si B ⊆ Y, se define f−1(B) = {x ∈ X | f(x) ∈ B}.

(i) Si A ⊆ X, probar que A ⊆ f−1(f(A)).

(ii) Probar que f es injectiva si y solo si A = f−1(f(A)) para todo A ⊆ X.

(iii) Si B ⊆ Y, probar que f(f−1(B)) ⊆ B.

(iv) Probar que f es suprayectiva si y solo si f(f−1(B)) = B para todo B ⊆ Y.

3. Sea f : X → Y una aplicación. Si A y B son subconjuntos de X, probar que f(A ∪ B) = f(A) ∪ f(B) y f(A ∩ B) ⊆ f(A) ∩ f(B). Probar que f(A ∩ B) = f(A) ∩ f(B) para todos los subconjuntos A, B ⊆ X si y solo si f es inyectiva.

4. Una aplicación f : X → Y es invertible izquierda si existe g : Y → X tal que g ∘ f = 1X. Se dice que f es invertible derecha si existe g : Y → X tal que f ∘ g = 1Y. Probar que f es inyectiva si y solo si f es invertible a izquierda. Probar que f es suprayectiva si y solo si f es invertible a derecha.

(Nota: Para probar que si f es suprayectiva entonces f tiene inversa a derecha necesitamos el llamado axioma de elección. El axioma de elección afirma que si X es un conjunto cuyos elementos son conjuntos no vacíos, entonces es posible elegir un elemento de cada uno de esos conjuntos. Esto que parece algo obvio, no lo es. Por ejemplo, el axioma de elección es equivalente al teorema del buen orden que establece que cualquier conjunto posee una relación de orden tal que todo subconjunto no vacío tiene menor elemento. También es equivalente al llamado lema de Zorn, una de cuyas aplicaciones es que todo espacio vectorial tiene base. Nadie ha encontrado jamás explícitamente un buen orden en ℝ. En definitiva, todo matemático debe plantearse alguna vez si acepta el axioma de elección o no. Nuestro consejo es aceptarlo y seguir adelante).

5. Sean A y B conjuntos. Probar que existe f : A → B inyectiva si y solo si existe g : B → A suprayectiva.

(Ayuda: Aplicar el problema 1.4).

6. Sea f : A → B una aplicación. Probar:

(i) f es inyectiva si y solo si para todo par de aplicaciones h, g : X → A tales que f ∘ g = f ∘ h, entonces g = h.

(ii) f es suprajectiva si y solo si para todo par de aplicaciones h, g : B → X tales que g ∘ f = h ∘ f, entonces g = h.

7. Sean f : A → B y g : B → C aplicaciones biyectivas. Probar que

(g ∘ f)−1 = f−1 ∘ g−1.

(Nota: A veces este se denomina el Dressing-Undressing Principle, pues nos desvestimos en orden opuesto al que nos vestimos).

8. Sean f : A → B y g : C → D aplicaciones. Se define la aplicación producto f × g : A × C → B × D como (f × g)((x, y)) = (f(x), g(y)). Estudiar cuándo f × g es inyectiva o suprayectiva en función de f y de g.

9. Para cada una de las siguientes relaciones sobre ℤ probar si son relaciones de equivalencia y en caso afirmativo, describir las clases de equivalencia.

(i) R = {(x, y) ∈ ℤ2 | x + y < 3}.

(ii) R = {(x, y) ∈ ℤ2 | x + y es par}.

(iii) R = {(x, y) ∈ ℤ2 | x = y o x = −y}.

(iv) R = {(x, y) ∈ ℤ2 | y = x + 1}.

10. En el conjunto ℤ × ℤ×, donde ℤ× = ℤ − {0}, decimos que (a, b) y (c, d) están relacionados si ad = bc. Probar que esta relación es de equivalencia.

(Nota: Los números racionales se definen como las clases de equivalencia de esta relación).

11. Sea n > 0 un entero. Definimos la siguiente relación en ℤ. Decimos que a, b ∈ ℤ están relacionados si n divide a a − b. Probar que esta relación es de equivalencia y que la clase de equivalencia de a es

a + nℤ = {a + nz | z ∈ ℤ}.

12. Probar que las siguientes aplicaciones son biyectivas:

(i) f : ℕ× → P = {2, 4, 6, …} y g : ℕ× → I = {1, 3, 5, …} dadas por f(n) = 2n y g(n) = 2n − 1. Concluir que el conjunto de números pares e impares positivos son numerables.

(ii) Si m ∈ ℕ×, la aplicación f : ℕ× → {n ∈ ℕ× | n > m} dada por f(n) = n + m.

(iii) f : ℕ× → ℤ dada por f(n) = n/2 si n es par, y f(n) = (1 − n)/2 si n es impar. Concluir que ℤ es numerable.

(iv) f : ℕ× × ℕ× → ℕ× dada por f(n, m) = 2n−1(2m − 1).

13. Si f : A → B es suprayectiva y A es numerable, entonces B es finito o numerable.

(Nota: Se pueden aplicar el problema 1.5 y el corolario 1.11. También podemos construir g : B → A inyectiva utilizando el teorema del buen orden en ℕ. Como A es numerable, entonces A está bien ordenado. Si b ∈ B, sea a el menor elemento de f−1({b}) y podemos definir g(b) = a).

14. Sea A un conjunto numerable y sea B un conjunto. Probar las siguientes propiedades.

(i) Si B es finito, entonces A − B es numerable.

(ii) Si B es finito, entonces A ∪ B es numerable.

(iii) Si B es numerable, entonces A ∪ B es numerable. Concluir por inducción que la unión de un número finito de conjuntos numerables es numerable.

(iv) Si B es numerable, entonces A × B es numerable. Concluir por inducción que el producto cartesiano de un número finito de conjuntos numerables es numerable.

(Ayuda: Para (i), utilizar el teorema 1.10. Para (ii), podemos suponer por (i) que A ∩ B = ∅. Si B tiene m elementos, sabemos por el problema 1.12 (ii) que existe f : {n ∈ ℕ× | n > m} → A biyectiva. Para (iii), por el mismo problema existen f : P → A y g : I → B biyectivas. Aplicar el problema 1.13. Para (iv), aplicar el problema 1.12 (iv)).

15. Probar que ℚ es numerable, utilizando que f : ℤ × ℤ× → ℚ, definida por f(n, m) = n/m, es suprayectiva.

16. Si An es finito o numerable para todo n ∈ ℕ×, probar que

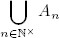
es finito o numerable.

(Ayuda: Por hipótesis, existe fn : ℕ× → An suprayectiva. Definimos

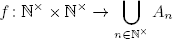
dada por f(n, m) = fn(m). Probar que f es suprayectiva).

17. Sea ℚ[x] el conjunto de los polinomios con coeficientes en ℚ.

(i) Probar que ℚ[x] es numerable.

(ii) Un número complejo α es algebraico sobre ℚ si existe un polinomio 0 ≠ f con coeficientes en ℚ, tal que f(α) = 0. Utilizando que todo polinomio f de grado n tiene (como mucho) n ráıces complejas, probar que el conjunto de los números algebraicos es numerable.