- -
- 100%
- +
C) 18
D) –7
E) –34
6. El resultado de la expresión 2 • (–3)2 + (–45) : (–3)2 – (–2) • (–1)7 es:
A) 1
B) 10
C) –12
D) –1
E) 11
7. Si a = –1, b = –2, c = –3 y d = –4, ¿cuál es el valor numérico de la expresión [–a + b • (d – c)] – a?
A) 4
B) 1
C) –1
D) 14
E) 16
8. Si a = –3, ¿cuál es el valor de –a3 – a2?
A) –36
B) –18
C) –15
D) 18
E) 36
9. Respecto del valor absoluto de un número real, ¿qué relación es falsa?
A) |–9| > |–8|
B) |–8| < – |–8|
C) |12| > |–10|
D) –|7| < |0|
E) –|1| > – |–7|
10. ¿Cuál es el resultado de la expresión 30 – 24 + 33 – 51?
A) 7
B) 6
C) –4
D) 39
E) –3
11. El rectángulo de la figura representa una cartulina en la que se quieren poner fotografías cuadradas de igual tamaño hasta cubrirla exactamente sin que estas se superpongan. ¿Cuál es la mayor longitud del lado de las fotografías que cumplen esta condición?
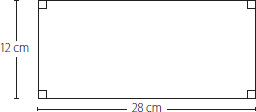
A) 3 cm
B) 4 cm
C) 5 cm
D) 6 cm
E) 7 cm
12. Cinco números enteros consecutivos suman cero. ¿Cuál es el menor de ellos?
A) 1
B) 0
C) –1
D) –2
E) –3
13. Si A , B , C y D son números enteros tales que B > A, B < D, B > C y A < C, ¿cuál es el orden decreciente de dichos números?
A) D > C > B > A
B) D > C > A > B
C) D > B > C > A
D) A > B > C > D
E) D > B > A > C
14. Si x y x < –1, ¿cuál(es) de las siguientes expresiones es (son) menor(es) que 1?
I. –x3
II. x5
III. 8x2
A) Solo I
B) Solo II
C) Solo III
D) Solo I y II
E) I, II y III
15. Se define: “Dos números son compatibles si el cociente entre el mayor y el menor es un número entero múltiplo de 3”. De acuerdo con esta definición, ¿cuál de los siguientes pares de números son compatibles?
A) 12 y 3
B) 60 y 12
C) 33 y 3
D) 54 y 27
E) 72 y 12
16. El valor de x en la igualdad –{4 –[12 – (5 + x)]} = 0 es:
A) 3
B) 2
C) 1
D) –2
E) –3
17. Si b es el antecesor de a, entonces (a + b)(a – b) – (a – b)2 es:
A) –2a
B) 2a – 1
C) 2a – 2
D) 2a + 1
E) 2a + 2
18. Si a, b, c con la condición de que a = 0, b < a y c > a, ¿cuál de las siguientes relaciones es falsa?
A) a : b = 0
B) b • c < 0
C) a + b < 0
D) c : b > 0
E) c – a > 0
19. En la expresión a + b + c = 2p, se sabe que a = 2, b = 5 y c = –3. ¿Cuál es el valor numérico de la expresión p2(p + a)(p + b)(p – c)?
A) –56
B) –112
C) 280
D) 112
E) 560
20. A las nueve de la mañana de un día, la temperatura fue de –4 ºC y a las tres de la tarde, de 5 ºC. ¿Cuánto varió la temperatura?
A) –9 ºC
B) 9 ºC
C) 1 ºC
D) –1 ºC
E) 10 ºC
21. Si a y b son números enteros consecutivos tales que a < b, entonces siempre se cumple que:
I. a : b = 1
II. a + b < 1
III. a • b = a2 + a
A) Solo I
B) Solo II
C) Solo III
D) Solo I y II
E) Solo II y III
22. Si 4.3N1 representa un número entero de 4 cifras divisible por 3, ¿qué valores puede tener el dígito N para que se cumpla la divisibilidad?
A) {1, 4, 7}
B) {1, 3, 5}
C) {1, 2, 3}
D) {1, 4, 8}
E) {1, 4, 9}
23. Sean M, N, Q tres números enteros distintos, tales que M > N > 0, Q = 0. ¿Cuál de las siguientes proposiciones es falsa?
A) QN + M > 0
B) MQ – NQ = 0
C) M : N + Q > 0
D) MNQ – MN < 0
E) Q – M + N > 0
24. Se sabe que X > Y > Z y una persona debe reunir $ X. Primero reúne $ Y y luego gasta $ Z. ¿Cuánto le falta para completar la suma requerida?
A) $ (Y + X + Z)
B) $ (Y – Z + X)
C) $ (–X – (Z – Y))
D) $ (Z + X – Y)
E) $ (X – (Y + Z))
25. Se tiene que n es múltiplo de 3. Entonces, ¿cuál(es) de las siguientes afirmaciones es (son) verdadera(s)?
I. n : 3 es múltiplo de 3.
II. 27n es múltiplo de 3.
III. n + 84 es múltiplo de 3.
A) Solo I
B) Solo II
C) Solo III
D) Solo I y II
E) Solo II y III
26. La relación x > y > z, con x, y, z se cumple si:
(1) x > z, y > z
(2) x > y
A) (1) por sí sola.
B) (2) por sí sola.
C) Ambas juntas, (1) y (2).
D) Cada una por sí sola, (1) o (2).
E) Se requiere información adicional.
27. Si x , ¿x < 0?
(1) x3 es negativo.
(2) –x es positivo.
A) (1) por sí sola.
B) (2) por sí sola.
C) Ambas juntas, (1) y (2).
D) Cada una por sí sola, (1) o (2).
E) Se requiere información adicional.
28. Si x, y , ¿x + y es impar?
(1) x – y es impar.
(2) xy = 6
A) (1) por sí sola.
B) (2) por sí sola.
C) Ambas juntas, (1) y (2).
D) Cada una por sí sola, (1) o (2).
E) Se requiere información adicional.
29. La expresión x3 – x tiene un único valor numérico si:
(1) x > 0
(2) x2 – 9 = 0
A) (1) por sí sola.
B) (2) por sí sola.
C) Ambas juntas, (1) y (2).
D) Cada una por sí sola, (1) o (2).
E) Se requiere información adicional.
30. Se puede determinar la cantidad total de personas, entre hombres y mujeres, que asisten a una fiesta si:
(1) es posible formar 15 parejas (hombre y mujer) entre los presentes y quedan 5 hombres sin pareja.
(2) la cantidad de hombres es mayor que la cantidad de mujeres.
A) (1) por sí sola.
B) (2) por sí sola.
C) Ambas juntas, (1) y (2).
D) Cada una por sí sola, (1) o (2).
E) Se requiere información adicional.
Respuestas correctas


Instrucciones
1. Este test tiene 30 preguntas. Cada una con 5 opciones, señaladas con las letras A, B, C, D y E, de las cuales una sola es la respuesta correcta.
2. Dispones de 60 minutos para responderlo.
1. El resultado de la expresión es:
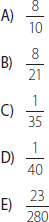
2. Una fracción con numerador y denominador positivo aumenta su valor si:
I. El numerador aumenta.
II. El denominador aumenta.
III. El denominador disminuye.
A) Solo I
B) Solo II
C) Solo III
D) Solo I y II
E) Solo I y III
3. En un curso de 40 estudiantes, los del total son niños. Si a mediados de año ingresan al curso 5 niñas, ¿cuál es la fracción, respecto del total, que representa a las niñas del curso?
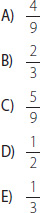
4. Una barra de aluminio mide 0,8 m. Por efecto de los cambios de temperatura, luego de 15 horas aumentó en una milésima parte su longitud. ¿Cuál es su medida?
A) 0,81 m
B) 0,88 m
C) 0,801 m
D) 0,8008 m
E) 0,8001 m
5. Si n es un número entero negativo distinto de –1, ¿cuál de las siguientes fracciones es la menor?
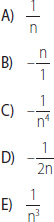
6. Si , entonces, ¿cuál(es) de las siguientes afirmaciones es (son) verdadera(s)?
I. b • c < a2
II. (a • b)–1 < c
III.
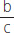
A) Solo I
B) Solo II
C) Solo III
D) Solo II y III
E) I, II y III
7. En un triángulo rectángulo isósceles, ambos ángulos interiores agudos disminuyen en un tercio su medida. Entonces la medida del tercer ángulo interior del triángulo resultante debe:
A) disminuir a su tercera parte.
B) aumentar en su tercera parte.
C) disminuir en sus dos terceras partes.
D) aumentar en sus dos terceras partes.
E) aumentar en su novena parte.
8. En un triángulo ABC, uno de sus ángulos interiores mide x , otro mide 30º más que la mitad de x y el tercer ángulo mide la tercera parte de x aumentado en 18º. ¿Cuál es la diferencia entre el mayor y el menor ángulo interior del triángulo ABC?
A) 72º
B) 24º
C) 30º
D) 42º
E) 66º
9. Un estanque tiene ocupada sus tres cuartas partes con agua. Si se le agregan 500 litros, el agua ocupa hasta los cinco sextos del estanque. ¿Cuál es su capacidad?
A) 6.000 litros.
B) 5.500 litros.
C) 4.500 litros.
D) 4.000 litros.
E) 3.500 litros.
10. Un partido de fútbol se desarrolla en dos tiempos de 45 minutos cada uno. ¿Qué fracción del tiempo que dura un partido queda cuando han transcurrido 15 minutos del segundo tiempo?
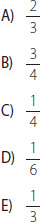
11. En un grupo de personas, de ellas no tienen hijos, un tercio tiene mellizos y las 35 personas restantes tienen solo un hijo. ¿Cuántas personas forman el grupo?
A) 70 personas.
B) 75 personas.
C) 60 personas.
D) 120 personas.
E) No se puede determinar.
12. En un curso, un día faltaron a clases de los estudiantes. Si ese día asistieron 35 estudiantes, ¿cuántos alumnos componen el curso?
A) 36 alumnos.
B) 38 alumnos.
C) 40 alumnos.
D) 45 alumnos.
E) 48 alumnos.
13. ¿Qué precio tiene una mercadería si los de los de ella equivalen a $ 5.600?
A) $ 15.000
B) $ 18.000
C) $ 21.000
D) $ 28.000
E) $ 42.000
14. Se tienen 13 botellas de L, de las cuales 7 están llenas y 6 a la mitad. ¿Cuántas botellas de L se necesitan para envasar la misma cantidad de litros?
A) 9 botellas.
B) 12 botellas.
C) 14 botellas.
D) 15 botellas.
E) 18 botellas.
15. Una persona compró cuatro séptimos de docenas de naranjas. ¿Cuántas naranjas compró?

16. Si a cuatro enteros dos quintos se le suma el producto de cuatro sextos por tres medios, se obtiene:
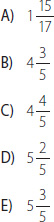
17. Si , ¿qué alternativa representa el orden entre ellas?
A) x < y < z
B) x > y > z
C) z > y > x
D) y < x = z
E) x = z < y
18. Los números racionales ordenados de mayor a menor son:
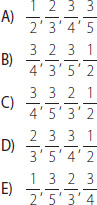
19. ¿Cuántos paquetes de kg de azúcar se pueden formar con 4 sacos de 30 kg cada uno?
A) 90 paquetes.
B) 120 paquetes.
C) 160 paquetes.
D) 180 paquetes.
E) 210 paquetes.
20. ¿Cuál es la expresión truncada a la décima del número 94,177?
A) 94
B) 94,1
C) 94,2
D) 94,17
E) 94,18
21. es igual a:
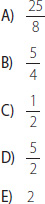
22. ¿Cuánto es la tercera parte del inverso multiplicativo del número 5?
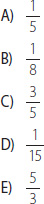
23. Si , entonces, de las siguientes expresiones, ¿cuál(es) resulta(n) un número entero?
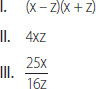
A) Solo I
B) Solo II
C) Solo III
D) Solo II y III
E) Solo I y II
24. El resultado de es:
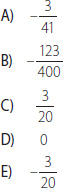
25. Un basquetbolista practica lanzamientos: convierte m y falla n. ¿Qué fracción del total de lanzamientos falla?
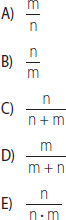
26. ¿Cuál es el precio de kg de manzanas?
(1) 3 manzanas tienen un precio de $ 270.
(2) 3 kilogramos y medio tienen un precio de $ 2.625.
A) (1) por sí sola.
B) (2) por sí sola.
C) Ambas juntas, (1) y (2).
D) Cada una por sí sola, (1) o (2).
E) Se requiere información adicional.
27. Si a , b y c son tres números racionales positivos, ¿cuál es el mayor?
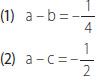
A) (1) por sí sola.
B) (2) por sí sola.
C) Ambas juntas, (1) y (2).
D) Cada una por sí sola, (1) o (2).
E) Se requiere información adicional.
28. La fracción es positiva si:
(1) p + q > 0
(2) p > 0
A) (1) por sí sola.
B) (2) por sí sola.
C) Ambas juntas, (1) y (2).
D) Cada una por sí sola, (1) o (2).
E) Se requiere información adicional.
29. Si , ¿cuál es el valor de c?
(1) a – c = 1
(2) 2a = 10
A) (1) por sí sola.
B) (2) por sí sola.
C) Ambas juntas, (1) y (2).
D) Cada una por sí sola, (1) o (2).
E) Se requiere información adicional.
30. Sean x e y números enteros distintos de cero. La fracción representa un número entero positivo si:
(1) x e y tienen el mismo signo.
(2) x > 0, e y es múltiplo positivo de x.
A) (1) por sí sola.
B) (2) por sí sola.
C) Ambas juntas, (1) y (2).
D) Cada una por sí sola, (1) o (2).
E) Se requiere información adicional.
Respuestas correctas


Instrucciones
1. Este test tiene 30 preguntas. Cada una con 5 opciones, señaladas con las letras A, B, C, D y E, de las cuales una sola es la respuesta correcta.
2. Dispones de 60 minutos para responderlo.
1. El resultado de la expresión es:

2. Si n es un número entero positivo, entonces la expresión representa siempre:
A) un número impar.
B) un número par.
C) una fracción equivalente a la unidad.
D) una fracción propia.
E) una fracción impropia.
3. ¿Cuáles fracciones son equivalentes entre sí?

A) Solo I y II
B) Solo II y III
C) Solo I, III y IV
D) Solo I, II y III
E) I, II, III y IV
4. El resultado de la expresión – 23 : 42 es:
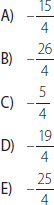
5. Al resolver la expresión 0,0000002 • 5 • 104 resulta:






