- -
- 100%
- +
E) log16 existe y su valor es 6.
13. Si P = log72, Q = log73 y R = log75, ¿cuál de las siguientes expresiones es igual a log735 – log730?
A) 8R – P + Q
B) 7 + R – P – Q
C) 7 – P – Q
D) 1 – P – Q
E) 1 – P – Q – R
14. ¿Cuál es el valor de la expresión log2112?
A) 7 • log 16
B) 16 • log27
C) 4 + log27
D) 6
E) 4 • log27
15. ¿Cuál de las siguientes afirmaciones es verdadera?
A) El logaritmo de un producto es igual al producto de los logaritmos.
B) El valor del logaritmo cuya base es igual al argumento es siempre igual a 0.
C) El logaritmo de una suma es igual a la suma de los logaritmos.
D) La solución de una ecuación logarítmica se debe remplazar en la ecuación original para comprobar que sus logaritmos estén bien definidos.
E) La base de un logaritmo puede ser 1.
16. ¿Cuál es el valor de la expresión log464 + log 1.000 – log7343?
A) –3
B) –1
C) 0
D) 3
E) 6
17. Si log 2 ≈ 0,30 y log 3 ≈ 0,47, ¿cuál es el valor de la expresión log 72 + log 36 – log 12?
A) 0,17
B) 0,77
C) 1,41
D) 1,54
E) 2,31
18. ¿Cuál es resultado de log7?

19. ¿Cuál es el valor de la expresión log42 • log4256?
A) log4128
B) log4258
C) log4512
D) 2
E) 8
20. Si log 2 ≈ 0,30 y log 3 ≈ 0,47, ¿cuál es el valor de la expresión log 64 + log 27 – log 36?
A) 0,77
B) 1,41
C) 1,67
D) 1,80
E) 3,55
21. ¿Cuál(es) de las siguientes igualdades es (son) siempre verdadera(s)?
I. logb(p + q) = logbp • logbq
II. logaa – logbb = 0
III.

A) Solo I
B) Solo II
C) Solo III
D) Solo II y III
E) Solo I y II
22. ¿Cuál de las siguientes expresiones equivale a log (x – 4) + log (x2 – 16) – 2 • log (x + 4)?
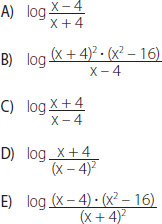
23. Para determinar el diámetro d (km) de un asteroide los astrónomos utilizan la fórmula: log d = 3,7 – 0,2 • g, donde g es su magnitud absoluta.¿Cuál es la magnitud absoluta de un asteroide si su diámetro mide 10 km?
A) –2,65
B) 1,04
C) 7,5
D) 23,5
E) 13,5
24. ¿Cuál de las siguientes expresiones equivale a 2 • log (x – 3) + log (x2 – 9) – log (x + 3)?

25. ¿Cuál de las siguientes igualdades representa una propiedad de los logaritmos?
A) logb(p • q) = logbp • logbq
B) logb(p + q) = logbp + logbq
C) logb(p + q) = logbp • logbq
D) logb(p • q) = logbp + logbq
E) logb(p – q) = logbp – logbq
26. ¿Cuál es la solución de la ecuación log (x + 4) = log (2x – 1)?
A) –5
B) –1
C) 0
D) 1
E) 5
27. ¿Cuál es el valor de x en la expresión logx64 = 3?
A) 1
B) 2
C) 3
D) 4
E) 5
28. ¿Cuál(es) de las expresiones siguientes es (son) igual(es) a log 2 + log 22?
I. 3 log 2
II. log 23
III. log 2 • log 22
A) Solo I
B) Solo II
C) Solo I y II
D) Solo II y III
E) I, II y III
29. Si a y b – {1}, entonces logba = c si:
(1) bc = a
(2) c > 0
A) (1) por sí sola.
B) (2) por sí sola.
C) Ambas juntas, (1) y (2).
D) Cada una por sí sola, (1) o (2).
E) Se requiere información adicional.
30. Si a, b , ambos distintos de uno, se puede determinar el valor de logba si se conoce que:
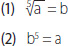
A) (1) por sí sola.
B) (2) por sí sola.
C) Ambas juntas, (1) y (2).
D) Cada una por sí sola, (1) o (2).
E) Se requiere información adicional.
Respuestas correctas


Instrucciones
1. Este test tiene 30 preguntas. Cada una con 5 opciones, señaladas con las letras A, B, C, D y E, de las cuales una sola es la respuesta correcta.
2. Dispones de 60 minutos para responderlo.
1. ¿Qué igualdad es falsa?
A) i523 = –i
B) i234 = –1
C) i65 = i
D) i72 = i
E) i122 = –1
2. Al resolver x2 + 75 = 0, ¿cuáles son las soluciones?

3. ¿Cuál es el resultado de la expresión ?
A) 2
B) 2i
C) 5i
D) –2
E) –2i
4. ¿Cuál(es) de las siguientes afirmaciones es (son) verdadera(s)?
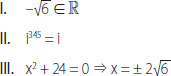
A) Solo I
B) Solo II
C) Solo III
D) Solo I y II
E) I, II y III
5. Respecto de los números complejos , ¿qué afirmación es falsa?
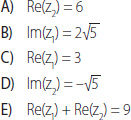
6. Si w , Im(w) = –5 y Re(w) = 15, ¿cuál es el número complejo w?
A) –5 + 15i
B) 15 + 5i
C) 15 – 5i
D) 5 – 15i
E) –15 – 5i
7. Considerando z1 = 3 + (y + 5)i, z2 = (3 – x) + 12i, para que z1 = z2, ¿cuáles deben ser los valores de x e y?
A) x = 3, y = 7
B) x = 6, y = 17
C) x = 3, y = 17
D) x = 0, y = 7
E) x = 0, y = 17
8. ¿Cuál es el conjugado del número complejo que se representa en el gráfico?
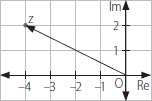
A) 4 + 2i
B) 4 – 2i
C) –4 + 2i
D) –4 – 2i
E) –2 – 4i
9. Considerando el gráfico de la pregunta 8, ¿cuál(es) de las siguientes igualdades es (son) verdadera(s)?

A) Solo II
B) Solo III
C) Solo I y II
D) Solo II y III
E) I, II y III
10. ¿Cuál(es) de las siguientes afirmaciones es (son) verdadera(s)?
I. Si z1 = 7 – 5i ⇒ Im(z1) = –5.
II. Si Re(z2) = –2, Im(z2) = 4 ⇒ z2 = –2 + 4i.
III. Si z1 = z2, z1 = a + 2i, z2 = 3 – bi, entonces a = 3 y b = 2.
A) Solo I
B) Solo II
C) Solo I y II
D) Solo II y III
E) I, II y III
11. Se definen los números complejos z1 y z2 como z1 = –10 – 5i y z2 = 8 + 4i. ¿Cuánto es z1 + z2?
A) –2 – i
B) 2 – i
C) –2 + i
D) 2 + i
E) –8 – i
12. En el plano de Argand se han representado los números complejos z1 y z2. ¿Cuánto es z1 + z2?
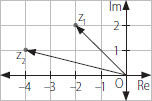
A) 6 + 3i
B) –6 + 3i
C) –6 – 3i
D) 3 + 6i
E) –2 + 3i
13. Considerando z = –1 + 2i, ¿cuál(es) de las siguientes igualdades es (son) verdadera(s)?
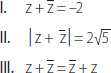
A) Solo I
B) Solo III
C) Solo II y III
D) Solo I y III
E) I, II y III
14. Si 4 – 5i + z = 9 + 8i, ¿cuál debe ser el número complejo z?
A) 5 – 3i
B) 5 + 13i
C) 5 + 3i
D) 5 – 13i
E) 5i + 13
15. Si z = 4 – 8i, ¿cuánto es el resultado de ?
A) 0
B) –4i
C) –8i
D) –16i
E) 8 – 16i
16. En el plano de Argand se han representado los números complejos z1 y z2. ¿Cuál es el resultado de z2 – z1?

A) 5 + i
B) 1 + 5i
C) –5 + 5i
D) –5 – i
E) 5 – i
17. Si 5 – 3i – w = 7 + 3i, ¿cuál es el número complejo w?
A) 2 – 6i
B) –2 – 6i
C) –2 + 6i
D) 2 + 6i
E) 2i – 6
18. Considerando z = 7 – 2i, ¿cuál(es) de las siguientes igualdades es (son) verdadera(s)?
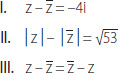
A) Solo I
B) Solo II
C) Solo III
D) Solo I y II
E) Solo I y III
19. Si z = 2 – i, w = 1 + i, ¿cuál es el resultado de z • w?
A) 3 + i
B) 3 – i
C) 3
D) –3 + 3i
E) –3 – 3i
20. Si z = 7 – 4i, ¿qué número representa a z–1?
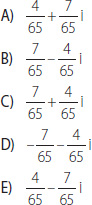
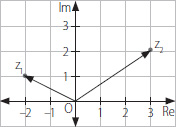
21. En el plano de Argand se han representado los números complejos z1 y z2. ¿Cuál(es) de las siguientes igualdades es (son) verdadera(s)?
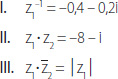
A) Solo I
B) Solo II
C) Solo I y II
D) Solo II y III
E) I, II y III
22. Si z = 3 – 5i, w = 6 + 2i, ¿cuál es el resultado de z : w?
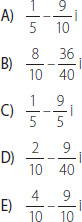
23. Se define . ¿Cuánto es |z|?
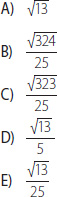
24. En la igualdad z(1 – i) = 2, ¿a cuánto equivale z–1?

25. En el plano de Argand se ha representado el número complejo z. ¿Cuánto es z5?


26. Respecto del número complejo z = –2 – 2i, ¿qué afirmación(es) es (son) verdadera(s)?
I. El módulo de z es

II. Re(z2) = 0.
III. Una de las raíces cuadradas de z es

A) Solo I
B) Solo II
C) Solo III
D) Solo II y III
E) I, II y III
Конец ознакомительного фрагмента.
Текст предоставлен ООО «ЛитРес».
Прочитайте эту книгу целиком, купив полную легальную версию на ЛитРес.
Безопасно оплатить книгу можно банковской картой Visa, MasterCard, Maestro, со счета мобильного телефона, с платежного терминала, в салоне МТС или Связной, через PayPal, WebMoney, Яндекс.Деньги, QIWI Кошелек, бонусными картами или другим удобным Вам способом.






