La pirámide visual: evolución de un instrumento conceptual

Euclides y el nacimiento de la pirámide visual

[Euclides], aparte de su genio, inventó una de las más grandes metáforas de la humanidad. Es como si, al despertar de un sueño, hubiese expresado: “La geometría es mi metáfora”

C. M. Turbayne (1962, p. 68)21

La breve descripción que hemos presentado de las escuelas extramisionistas e intramisionistas parece darle, en principio, toda la razón a Kuhn. Definitivamente, no se logró, en la Grecia antigua, un punto de vista unificado en torno a la naturaleza de la luz. Ninguna de las aproximaciones logró cautivar a la mayoría de investigadores como para que se empezara una elaboración paradigmática. Precisamente por eso, no se contó con criterios aceptados por la mayoría para discriminar entre, por un lado, soluciones bien encaminadas o acertadas a los problemas y, por otro, orientaciones sin autoridad o legitimidad alguna. Cada escuela rival abrazaba su propia metafísica y su propia teoría general del conocimiento, cada una cultivaba y protegía los fenómenos ópticos que esgrimía a su favor. Los diálogos, a lo sumo, se reducían a descalificar una cosmología, aduciendo la superioridad de la propia. ¿Podría esperarse progreso alguno en caso de perpetuarse esa dinámica? No creo que haya dificultad en conceder una respuesta negativa a la pregunta. En contraste con estos desencuentros, la gran invención de Euclides estableció un punto de acuerdo, un punto que hizo posible, como mostramos en la presente investigación, etapas de desarrollo progresivo, en el sentido de Lakatos. Aclaramos, sin embargo, que dichos acuerdos eludían preguntas básicas acerca de la naturaleza de la luz y del sensorio.

Dado que el punto de acuerdo que pretendemos desenterrar tiene que ver exclusivamente con el uso exitoso de un instrumento, mostramos que los compromisos ontológicos que ataban a los investigadores en el marco del programa a una u otra escuela eran por completo prescindibles. Ninguno de tales investigadores participó en el programa sin asumir compromisos ontológicos; no obstante, al examinar con cuidado sus aportes, es posible poner en evidencia que no se necesitaba de tales compromisos. El instrumento, como lo exponemos en este libro, podía ponerse en funcionamiento con el lenguaje y los compromisos ya sea de un extramisionista o de un intramisionista. Mostramos entonces que las pretendidas fases de progreso no tienen por qué explicarse en función de acuerdos ontológicos que hubiesen llegado a ser paradigmáticos. Más aún, sostenemos que la tensión entre adherentes a una u otra escuela se mantuvo como trasfondo de los debates y ello no constituyó óbice alguno para que el programa de investigación progresara, mientras mantenía firme el compromiso de conservar incólume el instrumento conceptual.

Entre los griegos se pueden distinguir tres ramas asociadas a los estudios ópticos: la óptica propiamente dicha, la catóptrica y la escenografía.22 La primera se ocupa de los rasgos geométricos asociados con la percepción visual; la segunda estudia tanto la reflexión de la luz en superficies pulidas (espejos planos o esféricos), como la refracción a través de medios diversos, y la tercera estipula técnicas bajo las cuales conviene dibujar las imágenes de los edificios para los instrumentos de utilería teatral.23

No existe un claro consenso entre los comentaristas a propósito de la autenticidad de las obras de óptica y catóptrica que se atribuyen a Euclides. Hay varios, y de hecho fuertes, indicios de que no se trata del mismo estilo del autor de Elementos. El más fuerte indicio tiene que ver con la comparación del rigor que se exhibe en Óptica (trad. en 2000a) y en Elementos (trad. en 1956), comparación que no favorece al primer escrito. No obstante, hay tan claros parecidos de familia en la forma de tratar los problemas, que podemos pensar que si la obra no es del mismo Euclides, el escrito debe pertenecer a un discípulo cercano. Sin mayores prevenciones, toda vez que no nos interesa hacer arqueología, pondremos en boca de Euclides todo aquello que se suscribe en los tratados referenciados.

Euclides, a pesar del lenguaje que usa en la presentación, no parece estar interesado en desentrañar las operaciones del alma que le permiten contemplar una imagen o un fantasma afín. Se interesa más por las apariencias que adquiere dicho fantasma. Por ello, en principio no es necesario tomar partido ora por una posición intromisionista, ora por una posición extramisionista. Su contribución puede usarse como esquema en cualquiera de las posiciones que queramos adoptar. Si bien es cierto que Euclides usa un lenguaje extramisionista, también habría podido recomendar el uso de la propuesta en un lenguaje intramisionista. Él ofrece, aunque no lo reconozca o lo sugiera, un esquema geométrico que es neutral frente al compromiso extra o intramisionista.

Podemos llegar a familiarizarnos con dicho esquema a la manera de un órgano o instrumento, que puede usarse como herramienta conceptual para perfilar, en una forma más clara, los problemas que atañen a la percepción. El tratado de Óptica es un compendio de 7 definiciones y 58 proposiciones derivadas. Las definiciones, que incluyen sin diferenciar postulados o axiomas, son, en su orden (Euclides, trad. en 2000a, pp. 135-136):

1. Las rectas trazadas desde el ojo se extienden a lo largo de grandes extensiones.

2. La figura, objeto de contemplación, se halla en la base del cono que tiene al ojo por vértice, y a las rectas desde allí trazadas, por el contorno del mismo.

3. Se ven los objetos en los que los rayos así trazados inciden y no se ven aquellos en los que dichos rayos no inciden.

4. Los objetos que se ven bajo un ángulo mayor parecen mayores; los que se ven bajo un ángulo menor, menores, y los que se ven bajo ángulos iguales, iguales.

5. Los objetos que se ven bajo ángulos más elevados parecen más elevados y los que se ven bajo ángulos más bajos parecen más bajos.

6. Los objetos que se ven bajo rayos más a la derecha parecen más a la derecha y parecen más a la izquierda los que se ven bajo rayos más a la izquierda.

7. Los objetos que se ven bajo un mayor número de rayos aparecen con mayor precisión.

El primer postulado, en reunión con el tercero, formula la propuesta en un lenguaje claramente extramisionista; sugiere que hay rayos visuales que emanan del ojo y nos permiten contemplar todos los objetos que caen en el interior del cono formado por dichos rayos. Esta, por ejemplo, es la valoración de Heath:

[La obra de Euclides] comienza de manera ortodoxa con definiciones, la primera de las cuales involucra la misma idea del proceso de visión que nosotros encontramos en Platón, esto es, que ella es debida a rayos que proceden de nuestros ojos e inciden sobre los objetos (1921/1981, vol. 1, p. 441).24

Aun cuando se trata de la lectura más cómoda, dado que acompañamos a Euclides en los compromisos ontológicos que parece asumir, no hay en el texto del geómetra algo que nos impida pensar que el cono pueda entenderse, y de hecho ser útil, a partir de rayos que se dirigen desde el objeto hasta el ojo. Mostramos, en el capítulo, que es posible hacer una lectura neutral del tratado, una lectura que no exija un compromiso ontológico en relación con los rayos que constituyen el cono visual. La primera definición habla de “rectas trazadas desde el ojo” como si aludiera a dibujos auxiliares, más que a la emanación de fluidos.

Es posible que esta neutralidad ontológica moleste al más férreo de los aristotélicos, que quisiera escudarse, por ejemplo, en el siguiente pasaje del estagirita: “mientras la geometría estudia la línea física, pero en tanto que no es física, la óptica estudia la línea matemática, no en tanto que matemática, sino en tanto que física” (Aristóteles, trad. en 1995, II, 194a10-11). Proponemos, pues, interpretar los rayos de Euclides, no en tanto rayos físicos, sino en cuanto instrumentos matemáticos que podrían interpretarse como el trayecto de efluvios que viajan o bien desde el ojo hasta el objeto, o bien desde el objeto hasta el ojo.

Con el ánimo de aligerar la presión que deviene del lenguaje extramisionista usado por Euclides, podemos esgrimir el hecho de que, en la primera definición, el autor introduce una cláusula hipotética y sugiere que los rayos visuales son trazos que podrían tener solo realidad en la imaginación. Veamos con atención cómo introduce el autor la definición mencionada: “Supóngase que las líneas rectas trazadas a partir del ojo se propagan a lo largo de un espacio de grandes magnitudes” (Euclides, trad. en 2000a, p. 135; las cursivas son nuestras). Así las cosas, la definición 1 puede parafrasearse en estos términos: “Demos por sentado que las líneas rectas que se trazan desde la vista se prolongan a una distancia de inmensas proporciones”.25

La definición 3 sugiere que vemos solo aquellos objetos opacos que interrumpen el trazo continuo de los rayos, es decir, aquellos objetos sobre los que inciden los rayos visuales. En el lenguaje intramisionista, tendríamos que decir que vemos aquellos objetos desde donde imaginamos líneas rectas trazadas hasta el ojo sin interrupción alguna; vemos el objeto si los rayos trazados desde él convergen en el ojo.

Las definiciones 4-7 sugieren que el tratado versa sobre cómo aparecen ante a mí los objetos visualmente perceptibles.

El texto es, entonces, un tratado de las apariencias visuales y de los instrumentos de control geométrico, a partir de los cuales emitimos juicios acerca de los objetos que activan dichas apariencias. Los objetos que delimiten una pirámide de mayor amplitud angular tienen, para el observador, la apariencia de objetos mayores, con independencia de si son realmente de menor tamaño, salvo que se hallan muy cerca del observador. La amplitud angular es el principal recurso geométrico para juzgar la apariencia.

El cono (o pirámide) de Euclides es un instrumento que comporta la siguiente combinación de elementos: 1) la propagación rectilínea de los rayos visuales, sin importar cuál es su naturaleza o la dirección de su propagación; 2) la transmisión inmediata de la información asociada a dichos rayos;26 3) el ojo se encuentra en el vértice del cono (o pirámide); 4) el objeto observado, o parte de él, ocupa la base del cono; 5) el tamaño aparente del objeto visto y su ubicación en el campo visual dependen, primero, de la amplitud angular del cono: si esta es mayor, mayor será el tamaño aparente del objeto; y, segundo, de la dirección del eje del cono;27 y 6) la claridad de la visión depende del número de rayos visuales que inciden sobre el objeto (o convergen sobre el ojo).

A partir de las siete definiciones (postulados), Euclides infiere 58 proposiciones. Hemos agrupado algunas de estas proposiciones en seis teoremas, que reúnen los resultados más importantes en el marco del programa de investigación de nuestro interés.

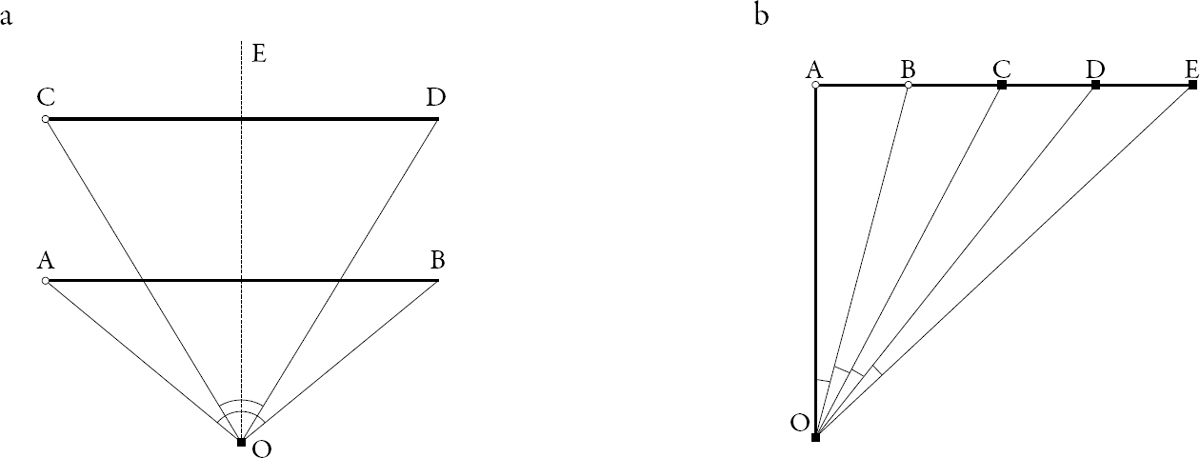
Figura 1.1. Teorema 1. a. Objetos similares a diferentes distancias; b. objetos similares desplazados lateralmente

Fuente: Elaboración del autor. Las figuras cuentan con modelación en el micrositio.

Teorema 1 (Proposiciones 4, 5, 7, 53, 56). Objetos de igual tamaño ubicados a distancias diferentes se despliegan con diferentes amplitudes angulares en nuestro campo visual. Los más alejados se contemplan bajo ángulos más pequeños y, en consecuencia, adquieren una apariencia de menor tamaño.

Aun cuando el segmento AB coincide en longitud con el segmento CD (véase figura 1.1a), AB parece mayor para el observador en O, toda vez que el ángulo AOB es mayor que el ángulo COD, siempre que CD esté más alejado de O que AB.28

La proposición 4 establece un resultado semejante, cuando los objetos de igual tamaño se organizan a lo largo de una misma recta y uno a continuación del otro. En este caso, si O presenta la ubicación del observador (véase figura 1.2b) y aun cuando las magnitudes de los segmentos son tales que

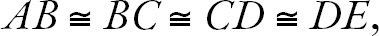
la apariencia varía, toda vez que

por lo tanto, AB parecerá mayor que BC, este que CD, y este que DE.29

La proposición 7 analiza el mismo caso cuando los segmentos, aunque están sobre la misma recta, no se encuentran uno a continuación del otro.

Teorema 2 (Proposición 6). Los espacios paralelos vistos de lejos parecen convergentes. Esta proposición reviste gran importancia, toda vez que anticipa uno de los principios centrales de la organización perspectiva, advertida por los pintores del Renacimiento.30

Euclides supone que las longitudes de los segmentos paralelos AC, FH, GI y BD son iguales y pide imaginar que A, F, G, B se encuentran en la misma recta AB, en tanto que C, H, I, D lo están en la recta CD (paralela a AB) (véase figura 1.2).

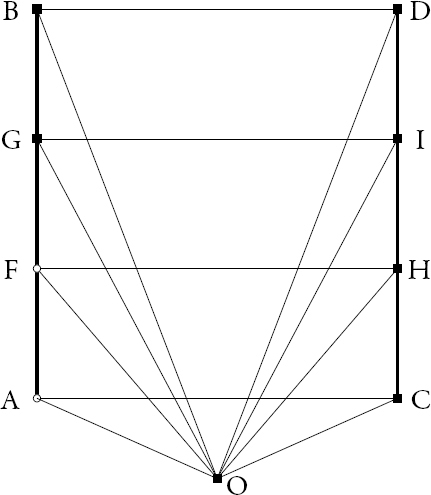
Figura 1.2. Teorema 2

Fuente: Elaboración del autor. La figura cuenta con modelación en el micrositio.

Dado que AC está más cerca del observador O que FH, y este más cerca que GI y GI más cerca que BD, debe ocurrir —en virtud del teorema anterior— que AC parece mayor que FH, este mayor que GI y GI mayor que BD. En consecuencia, los segmentos transversales, aunque de igual longitud, parecerán menores cuanto más lejos se encuentren del ojo O.

Así las cosas, las rectas paralelas AB y CD perderán la apariencia de paralelas y se verán en el campo visual de O como si fuesen convergentes.

De igual modo, si O se halla en un plano más elevado que el de ABDC, los resultados siguen siendo los mismos, en tanto que BD parecerá estar en una posición más elevada que GI, este segmento en una más elevada que FH y este en una más elevada que AC (teorema 4, proposición 10).

Teorema 3 (Proposición 8). Las dimensiones aparentes de los objetos no son inversamente proporcionales a las distancias de ellos al ojo. Podemos sentirnos inclinados a esperar, en primera aproximación, que un objeto ubicado n veces más lejos que otro de igual tamaño y en idéntica distribución con respecto al eje visual, aparezca en nuestro campo visual como si fuese n veces menor, como se asume en la representación perspectiva ideada en el Renacimiento. Este, sin embargo, no es el caso, si el tamaño aparente se juzga a partir de la amplitud angular del cono de Euclides.

Sean AB y CD dos objetos de idéntica longitud, ubicados perpendicularmente al eje visual OA y a distancias disímiles del observador O (véase figura 1.3). Euclides demuestra, en un lenguaje diferente al que transcribo aquí, que si AO = nCO, tan (β) = ntan (α); pero de allí no puede inferirse que β = nα, salvo si se trata de ángulos muy pequeños.

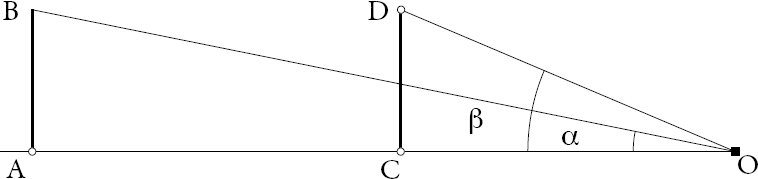
Figura 1.3. Teorema 3

Fuente: Elaboración del autor. La figura cuenta con modelación en el micrositio.

El comportamiento de la amplitud angular (trazo continuo) y de la tangente de dicha amplitud (trazo discontinuo) en relación con la distancia del objeto al observador puede apreciarse en la gráfica de la figura 1.4.31 La amplitud angular no es inversamente proporcional a la distancia (como sí lo es la tangente de dicha amplitud); salvo quizá, con cierto nivel de aproximación, para distancias grandes, para las cuales la amplitud angular es muy pequeña.

Erwin Panofsky ha llamado la atención acerca de la dificultad que introduce esta proposición en el marco de los esquemas conceptuales que orientan la perspectiva renacentista (1927/2003, pp. 19-20).

Teorema 4 (Proposiciones 10, 11, 13, 14). Cuando el ojo se encuentra en un plano diferente a los objetos que divisa, ocurre que si el ojo está por encima, los objetos más alejados parecerán más elevados, y si está por debajo, dichos objetos parecerán más bajos.

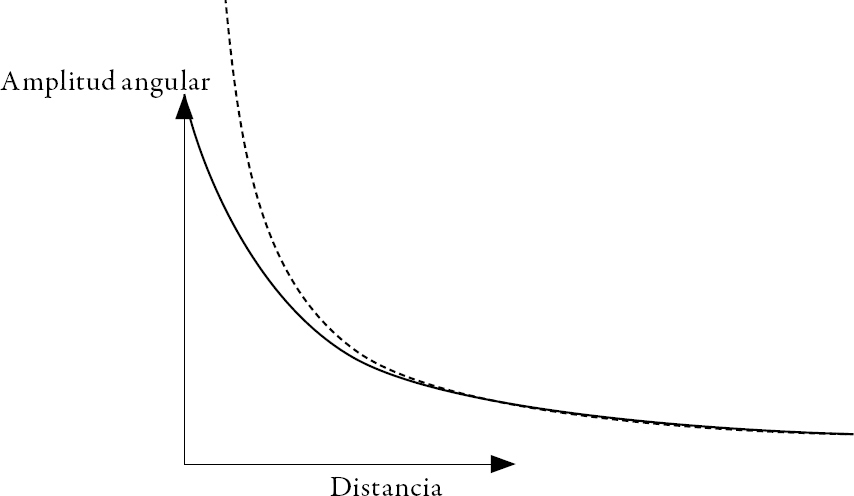
Figura 1.4. Comportamiento de la amplitud angular con la distancia

En trazo continuo se representa el comportamiento de la amplitud angular; en trazo discontinuo, el de la tangente de dicha amplitud.

Fuente: Elaboración del autor. La figura cuenta con modelación en el micrositio.

Supongamos que el observador O, desde un plano más elevado, contempla los puntos B, C, D sobre la misma recta, con D más alejado que B (véase figura 1.5). Al trazar los rayos visuales dirigidos a dichos puntos, el observador notará que cruzan la perpendicular a AD, trazada por Z, en el siguiente orden de abajo a arriba: B′, C′, D′. En forma análoga, al contemplar E, F, G desde un punto más bajo, los objetos más alejados aparecerán más bajos.

El razonamiento es interesante, toda vez que la recta ZE′ cumple el mismo papel que siglos más adelante desempeñará el velo de Alberti.32 También se puede advertir que el punto al que parece que convergen las paralelas AD y EG ha de encontrarse a la misma altura de O.

Teorema 5 (Proposiciones 22-27). Cuando observamos una esfera, ella tiene la apariencia de un círculo en un plano perpendicular a la recta que une el ojo y el centro de la esfera. Además, el radio de tal círculo es menor que el radio aparente que le hubiese correspondido a la esfera completa.

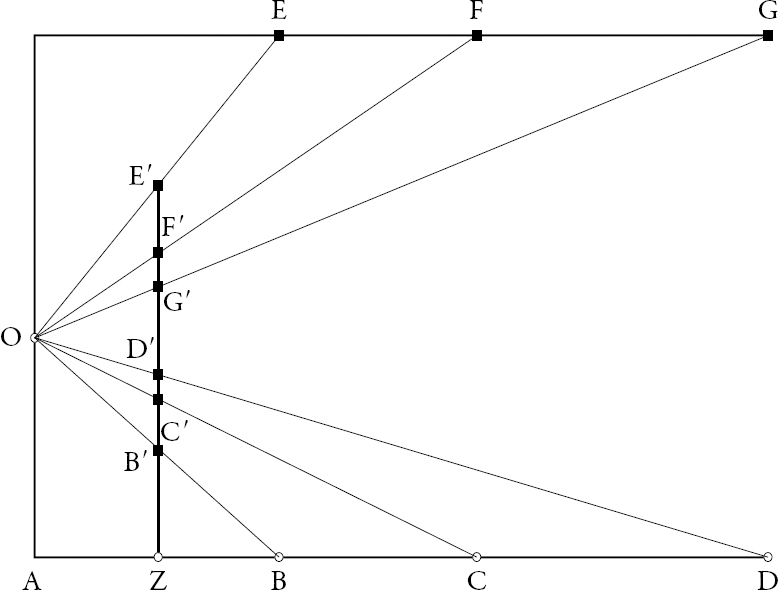
Figura 1.5. Teorema 4

Fuente: Elaboración del autor. La figura cuenta con modelación en el micrositio.

Imaginemos el observador en el punto O y la esfera de centro A, cuyo corte con uno de los planos que contiene la recta AO produce la circunferencia de radio AB (véase figura 1.6). La circunferencia de diámetro AO en el plano mencionado corta a la esfera en los puntos B y D, que son precisamente los puntos en los que OB y OD son tangentes a la esfera en el plano que hemos acotado.

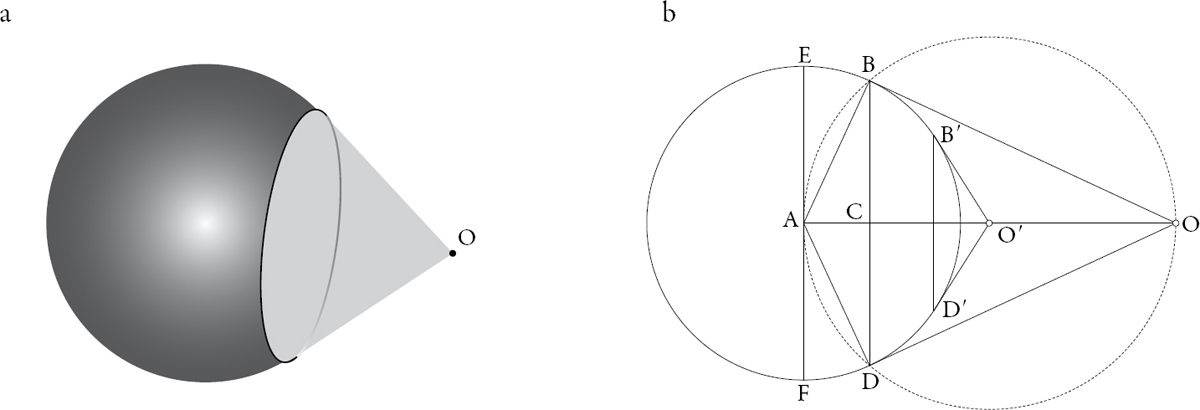
Figura 1.6. Teorema 5. a. Visión de una esfera; b. esfera reducida

Fuente: Elaboración del autor. Las figuras cuentan con modelación en el micrositio.

Si hacemos girar BC en torno al eje AO, surge un círculo en un plano perpendicular a AO. Este círculo determina la parte visible de la esfera para un observador en O. Ninguno de los puntos de la esfera entre B y E o D y F podrá ser visto, pues allí no incide ningún rayo que no sea oculto por el cono OBD (postulado 3).

Por otra parte, dado que BD es menor que EF, el diámetro del círculo aparente resulta menor que el diámetro de la esfera.

La proposición 22 sugiere que los puntos de la esfera entre B y D dan la apariencia de un segmento de recta en el plano perpendicular a AO. La argumentación es correcta si asumimos que la esfera está tan alejada que perdemos de vista la convexidad o no podemos apreciar matices singulares, como sombras o texturas en la superficie. Este teorema singular explica por qué el Sol y los planetas, pese a su esfericidad, se observan como discos circulares de diámetros menores que los que corresponderían a las semiesferas completas.33

Si O se acerca a la esfera, la diferencia de tamaños entre BD y EF es más acentuada (proposición 24). Si O′ es el nuevo punto de observación, la esfera se contemplará bajo el aspecto del círculo de diámetro B′D′, es decir, una porción más reducida de la semiesfera que la marcada por BD. Sin embargo, tendremos la ilusión de estar contemplando más, toda vez que el ángulo D′O′B′ es mayor que el ángulo BOD.

Teorema 6 (Proposiciones 34-36). La apariencia que una circunferencia da a un observador que la mira desde otro plano, depende de la ubicación de este. Si él se encuentra en un punto sobre la recta que, a partir del centro, es perpendicular al plano de la circunferencia, contemplará todos los diámetros bajo la misma amplitud angular; en consecuencia, el rasgo de circularidad se conserva.

Si el observador, en un plano diferente al de la circunferencia, se halla a una distancia del centro igual al radio de la misma, desde allí también se apreciarán todos los diámetros bajo la misma apariencia y, en consecuencia, el rasgo de circularidad así mismo se conservará.

Si OA es perpendicular al plano BECD (véase figura 1.7), no hay dificultad en advertir que el ángulo BOC es igual al ángulo DOE, y así para cualquier otro diámetro diferente. Entonces, un observador en O divisará todos los diámetros bajo la misma amplitud angular y por ello parecerán iguales (postulado 4).

Si OA no es perpendicular al plano, pero su longitud es igual a la de AB, el ángulo BOC será recto, sin importar el diámetro al cual hagamos referencia. En las posiciones restantes, los diámetros tendrán apariencias disímiles.

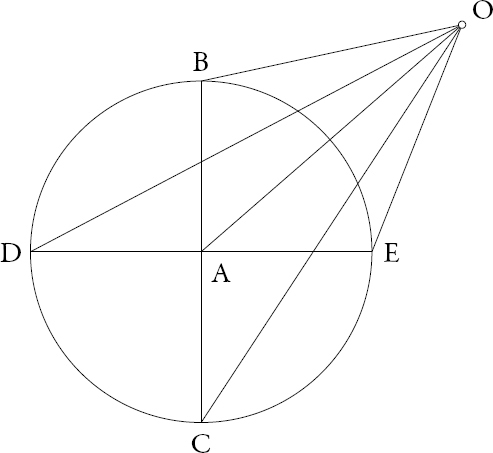
Figura 1.7. Teorema 6

Fuente: Elaboración del autor. La figura cuenta con modelación en el micrositio.

Hemos presentado un conjunto de ejemplos que muestran cómo se puede valorar la óptica de Euclides, como un canon que propone un lenguaje e instrumentos de control matemático para ofrecer explicaciones de fenómenos simples que estamos dispuestos a reunir bajo un inventario de situaciones familiares: 1) los objetos que se alejan disminuyen su apariencia en el campo visual; 2) cuando un observador se ubica entre segmentos paralelos de gran longitud, pero en un plano diferente, los observará como si tales segmentos se reunieran en un punto que se encuentra a la misma altura del observador; y 3) no es posible ver, en forma simultánea, todos los puntos de una esfera.

También podemos valernos del instrumento para anticipar teóricamente situaciones que podemos someter a evaluación empírica: 1) los tamaños aparentes de objetos de idéntica longitud no son inversamente proporcionales a sus distancias al observador; 2) el diámetro aparente de la sección observable de una esfera es menor que el diámetro que le correspondería en caso de verse completa; 3) una circunferencia que es vista por un observador ubicado en un lugar que no está en el mismo plano y, además, no se halla ni en la perpendicular al plano trazada desde el centro, ni en un lugar sobre la superficie esférica de radio igual al de la circunferencia, pierde la apariencia de circularidad; y 4) los objetos rectangulares vistos a gran distancia parecen curvarse en sus vértices (proposición 9).

En este marco de prescripciones teóricas hay también anomalías que demandan la intervención de los investigadores que acojan tales preceptos: 1) observamos el mundo con dos ojos, no con uno; y 2) dado que la única variable geométrica para establecer las dimensiones o la ubicación de un objeto que divisamos en nuestro campo visual se limita a la amplitud angular de la pirámide que lo abraza, debemos concluir que tamaño y distancia se encuentran indeterminados. Es decir, si conocemos de antemano la distancia a la que se halla el objeto, podemos anticipar sus dimensiones físicas, a partir de la amplitud angular de la pirámide (props. 18-21); o, por otra parte, si estamos familiarizados con las dimensiones físicas, podemos anticipar la distancia a la que se ubica, a partir de la amplitud angular de la pirámide (props. 48-49). Pero si desconocemos tanto la distancia a la que se halla un objeto como sus dimensiones físicas, no podremos anticipar esa información a partir de la amplitud angular de la pirámide visual: cuando observamos un objeto con el que no estamos familiarizados, no podremos anticipar si, dada la amplitud angular, divisamos un objeto de gran tamaño que está muy lejos, o un objeto menor que se halla muy cerca (véase figura 1.8).