La pirámide visual: evolución de un instrumento conceptual

Figura 1.8. Cómo es visto un camello por medio de un triángulo visual

Fuente: Edgerton (2009, p. 24). Dibujo de Edgerton.

Ptolomeo y la visión binocular

Nosotros, por lo general, contemplamos el mundo con dos ojos que cooperan. En ese orden de ideas, la pirámide visual nos ofrece un instrumento incompleto (o impreciso) que únicamente puede usarse en circunstancias restringidas. Así las cosas, o bien renunciamos al uso de la pirámide e insistimos en la búsqueda de otro lenguaje para plantear las preguntas asociadas con la percepción visual, o bien conservamos el lenguaje que sugiere el instrumento y procuramos modificaciones que le permitan adaptarse a la visión binocular.

Ptolomeo asumió la defensa del instrumento y logró introducir importantes modificaciones para hacer más rica su aplicación. Entre estas modificaciones, cabe mencionar: 1) crear métodos que permiten concebir una pirámide virtual, que sintetiza los aportes de las dos pirámides individuales pensadas una para cada ojo; 2) proponer criterios preliminares para concebir la formación de imágenes en espejos; 3) iniciar los estudios cuidadosos de la refracción de la luz, y 4) enfatizar el lenguaje que distingue los sensibles propios de los comunes.

Las hipótesis más confiables sugieren que Ptolomeo nació en una fecha cercana al año 100 d. C., en el seno de una familia greco-egipcia, y que, a juzgar por su peculiar nombre, “Claudio”, ostentaba el título de ciudadano romano. El tratado más influyente de Ptolomeo, y de hecho su primera obra,34 Almagesto, debió estar listo en el año 141 d. C. En dicho tratado, Ptolomeo llama la atención sobre uno de los problemas más debatidos en la Antigüedad, en relación con las paradojas de la percepción visual: el tamaño aparente del Sol y la Luna, cuando se contemplan en el horizonte (trad. en 1998, H13, p. 39).35

En las primeras páginas del libro I, Ptolomeo quiere convencer al lector de que el movimiento más apropiado para los objetos celestes es, precisamente, el movimiento circular, y defiende, entre otros, el siguiente argumento: si los objetos en el cielo tuviesen un movimiento diferente al circular con la Tierra en el centro, necesariamente las distancias medidas (o contempladas) desde la Tierra deberían variar; dado que dichas variaciones no son observadas, podemos confiar, entonces, en que el movimiento que más conviene a los astros es el circular. El argumento, sin embargo, debe enfrentar un problema: el Sol y la Luna parecen apreciablemente mayores cuando se contemplan en el horizonte y se comparan con la apariencia que exhiben en el punto más alto del cielo.

En principio, podríamos atribuir dicha variación a un cambio en la distancia y con ello tendríamos que alejarnos de la conveniencia de la circularidad. Ptolomeo ofrece una explicación que salva la conveniencia del movimiento circular:

El incremento aparente en sus tamaños en el horizonte es causado, no por la disminución de sus distancias, sino porque las exhalaciones de humedad que rodean la Tierra se interponen entre el lugar desde donde adelantamos la observación y la ubicación de los cuerpos celestes, justo como los objetos ubicados en el agua aparecen más grandes que lo que son, y en tanto más se sumergen, más grandes aparecen (trad. en 1998, H13, p. 39).

Ptolomeo advierte así la necesidad de considerar efectos de refracción de la luz no solo para salvar la circularidad del movimiento de los objetos celestes, sino también para ocuparse de la visión en general. En contraste con la explicación anterior, Ptolomeo, en el tratado Óptica, señaló serias limitaciones de dicha elucidación y prefirió abrir espacio a una de naturaleza psicológica. Este hecho sugiere que dicho tratado debió estructurarse más tarde que Almagesto.

Los comentaristas que atribuyen a Ptolomeo el compendio de óptica están de acuerdo en pensar que dicho tratado corresponde a los periodos de mayor madurez del autor y debe ubicarse entre los años 160 y 170 d. C. Hay evidencias de la existencia de versiones griegas del tratado de Ptolomeo hasta el siglo VI d. C.; también hay evidencias, a partir de algunos comentarios de Alhacén, de la circulación de una versión árabe a mediados del siglo IX d. C. La traducción del árabe al latín fue obra de Eugenio de Sicilia (ca. 1160 d. C.). Desafortunadamente, esta edición contaba con dos inmensas lagunas: la ausencia del libro I y la mutilación de fragmentos importantes del libro V.36

El tratado de Ptolomeo consta de cinco libros. El primero, desaparecido, debía ocuparse tanto de la manera como la luz y el flujo visual interactúan, como de las diferencias entre los dos.37 El segundo se dedica a las propiedades visibles (intrínsecas, primarias y secundarias) y ofrece interesantes explicaciones para el origen de algunas ilusiones ópticas. El tercero trabaja el tema de la reflexión y la formación de imágenes en espejos planos y en espejos convexos. El cuarto se encarga de los espejos cóncavos. El quinto, último e incompleto, pretende atender la refracción de los rayos visuales.

Crombie sostiene que Ptolomeo acogió el estilo matemático de Euclides y lo complementó con una exigencia de control experimental. El historiador formula su tesis en los siguientes términos:

Euclides y otros matemáticos aspiraron idealmente a desarrollar su investigación sobre los fenómenos [ópticos] de forma puramente teórica con su modelo geométrico o aritmético. Más tarde se dieron cuenta, como Ptolomeo en su Óptica, que al explorar fenómenos complejos, las hipótesis deben ser controladas por medio de la observación y el experimento, para decidir si un posible modelo teorético produce las consecuencias que aparecen en el mundo real (1986/1993, p. 38).

Crombie quiere ver en Ptolomeo a un investigador moderno, o a una anticipación de la Modernidad. Como veremos más adelante en este apartado, es cierto que Ptolomeo se vale provechosamente de la observación y de ciertos modelos de experimentación controlada. Pero no lo hace con la expectativa de tener la experimentación como norma de control de las especulaciones teóricas. La seguridad del uso de modelos geométricos se presupone antes de que la experiencia la autorice. El investigador acude a la experiencia, pero no lo hace con el temor de verse obligado a declinar en sus compromisos teóricos.

La actividad visual, asume Ptolomeo, percibe corporeidad, color, forma, tamaño, lugar, actividad y reposo.38 Aquella actividad exige dos condiciones: por un lado, se precisa de alguna iluminación y, por otro, algo opaco debe bloquear el paso del flujo visual. Aquello que bloquee el paso de la luz es lo que resulta ser intrínsecamente visible, se trata de un tipo de corporeidad (objetos compactos). Si, en lugar de bloquear, el objeto permite ser atravesado por el flujo visual, no nos percataremos visualmente de la existencia de dicho objeto interpuesto.

El color, por su parte, es primariamente visible, en el sentido de los sensibles propios de Aristóteles; pero no es intrínsecamente visible, atendiendo al carácter accidental del color y al hecho de que este solo puede captarse con presencia del flujo luminoso.39 El color, como defiende también Aristóteles, es una característica de las superficies del objeto compacto que se deja ver, no es una propiedad de la vida interna del cuerpo.

Las propiedades restantes son visibles en sentido secundario, pues se aprehenden atendiendo o bien los contornos del objeto coloreado (forma, tamaño), o bien un marco de relaciones entre objetos compactos coloreados (lugar, actividad, reposo).

La claridad de la percepción visual depende, entre otros factores, de la cantidad del flujo visual que es interceptado y de la forma como sucede dicha interceptación. Así, un objeto es visto con más claridad si recibe una mayor cantidad de flujo visual y si ello ocurre en la forma más directa posible, es decir, si los rayos inciden sobre el objeto de manera perpendicular. No obstante, cuando Ptolomeo pretende explicar por qué los objetos distantes se ven con menor claridad, prefiere atribuir ese hecho a que los rayos visuales se contaminan con algo de la oscuridad del aire que se interpone (Óptica, II, § 19). Como un corolario de las anteriores declaraciones, se infiere que lo que es visto por el rayo central —es decir, el rayo que coincide con el eje del cono visual— se contempla con la mayor claridad posible (Óptica, II, § 20).

A la distinción ontológica inicial entre el tipo de propiedades visuales, le acompaña una distinción epistemológica, que alude a la forma como aprehendemos las propiedades mencionadas. Citemos a Ptolomeo:

[…] debemos decir, primero, que todas las propiedades visibles intrínseca o primariamente son en efecto contempladas por medio de una pasión que surge con el flujo visual, mientras que las propiedades visibles en forma secundaria son vistas únicamente en virtud de accidentes que acompañan dicha pasión (Óptica, II, § 22).

Se puede decir que las primeras se nos imponen como dadas, en tanto que las segundas deben ser inferidas.

De esta manera, el análisis de la percepción visual supone, por un lado, una clarificación de las propiedades visibles que residen en los objetos y son disparadas por condiciones propias del ambiente circundante (iluminación) y, por otro, una elucidación de la facultad sensitiva misma. Aun cuando la pasión mencionada por Ptolomeo supone cierta actitud receptiva de la facultad sensible —en algún sentido pasiva—, el hecho mismo de percibir un objeto supone la integración de propiedades que vienen del objeto y propiedades que devienen de nuestra facultad receptiva.

En relación con el lugar en donde se capta la fuente que estimula la visión, Ptolomeo aduce que la distancia desde el objeto hasta el espectador se percibe a partir de una supuesta propiedad interna del rayo visual, a saber, su extensión. Lo que es visto a través de un rayo más extenso aparecerá como un objeto más alejado (Óptica, II, § 26). Así las cosas, ver un objeto distante es tocarlo con una prótesis que se puede extender y que deja un registro de qué tanto se ha extendido.40

Por otra parte, las dimensiones del objeto se perciben a través de la amplitud con que se despliegan los rayos visuales a lado y lado del eje del cono visual, siempre que este caiga sobre un punto medio del objeto que llama nuestra atención. Si disponemos de un bastón extensible para obtener reportes táctiles de los objetos que nos rodean, podemos pensar que entre más tengamos que extender el bastón para alcanzar un objeto, más lejos hemos de inferir su ubicación, y entre mayor sea la amplitud angular que permite recorrer su dimensión, más grande hemos de considerar el objeto.41

En caso de aceptar la propuesta de Ptolomeo, tendríamos resuelto, a diferencia de lo que ocurría en el modelo de Euclides, el problema de la indeterminación de distancia y tamaño del objeto: la extensión del rayo visual nos informa qué tan lejos se encuentra el objeto, y a continuación, a partir de esta información, más la amplitud de la pirámide visual que lo abraza, podemos inferir las dimensiones de la cara visible del objeto.

Imaginemos que el bastón aludido en la analogía anterior está ya en contacto con un objeto y no hemos tenido la oportunidad de percatarnos de la extensión de dicho bastón. En ese caso, sabremos de la presencia de un objeto que obstruye al bastón, pero carecemos de información acerca de lo distante o cercano que pueda encontrarse. Si yo puedo establecer la distancia del objeto es o bien porque conozco de antemano la dimensión del bastón (estoy familiarizado con ella), o bien porque tengo reportes cinestésicos de qué tanto he tenido que extender tal prótesis. Lo que resulta problemático en la explicación de Ptolomeo es que no hay, al menos en principio, análogo visual alguno para ninguna de estas dos opciones.

En resumen, la distancia del objeto al observador se percibe por medio de una propiedad intrínseca del rayo visual —su longitud—. Entre tanto, el tamaño del objeto se infiere a partir de una relación funcional compleja, que depende de tres variables: distancia entre objeto y observador, amplitud angular del cono visual que aprehende el objeto en su conjunto y disposición del objeto frente al observador.

Por “disposición” se entiende el arreglo con respecto al eje del cono visual: el objeto se encara frontalmente si él se dispone en forma perpendicular al eje, y se encara de manera oblicua si ese no es el caso.

Así las cosas, dos objetos que se perciban a igual distancia y frontalmente, lo harán de tal manera que aquel que se perciba bajo un ángulo mayor parecerá mayor. Si la distancia es idéntica y la amplitud angular es la misma, el objeto que parece menor será aquel que se acerque más a la disposición frontal. Si la amplitud angular es la misma y la disposición es frontal, el objeto más alejado parecerá mayor. En los casos intermedios es muy difícil establecer una regla general para la aprehensión de tamaños.42

El asunto puede tornarse más complejo si se toman en cuenta algunos de los factores adicionales que alteran nuestra percepción de la distancia o el tamaño. A manera de ejemplo, la percepción de la distancia puede verse afectada por el brillo con el que percibimos el objeto. Ptolomeo tan solo constata el hecho y no hace el menor esfuerzo por conciliar esta perspectiva con la orientación previa que pretendía sugerir que la distancia a la que se percibe el objeto depende exclusivamente de la longitud del rayo visual.

De cualquier manera, Ptolomeo deja un testimonio interesante de un conocimiento práctico empleado por los artistas para generar la ilusión de distancia. Ese conocimiento constituye una primitiva versión de la perspectiva cromática, mejorada siglos después por Leonardo da Vinci. “Los pintores murales”, informa Ptolomeo, “usan débiles y tenues colores para hacer aparecer las cosas que ellos quieren representar como si estuviesen distantes” (Óptica, II, § 124).

Nos detendremos ahora en el análisis de la visión binocular. Este hecho resume una anomalía que hacía razonable el abandono del instrumento. Sin embargo, abandonar un instrumento que había ya mostrado grandes logros habría sido insensato desde la perspectiva del programa de investigación. Con el ánimo de salvar el uso del instrumento, Ptolomeo propuso substituir las dos pirámides —una para cada ojo— por una pirámide media, de suerte que los teoremas demostrados en el marco del cono euclidiano fueran remitidos a esta nueva pirámide media. En resumen, se trata de substituir la visión binocular por la mirada de un cíclope estratégicamente ubicado. Este recurso requiere que se puedan concebir reglas de correspondencia entre la información recogida por cada pirámide individual y la información presente ante la pirámide del cíclope.

Cuando alguien mira con un ojo, cada objeto aparece en una ubicación determinada. Sin embargo, cuando alguien contempla un objeto con dos ojos, este aparecerá en una ubicación bien determinada solo si los ejes de cada uno de los dos conos visuales convergen en un mismo sector del objeto observado. Explica el filósofo:

Nosotros estamos naturalmente dispuestos para girar nuestros ojos inconscientemente en varias direcciones con un admirable y preciso movimiento, hasta que ambos ejes convergen sobre el medio de un objeto visible, y ambos conos forman una base singular sobre el objeto visible que ellos tocan (Óptica, II, § 28).43

Este hecho se corrobora con un simple experimento psicológico: si forzamos alguno de los dos ojos de tal manera que los ejes de los respectivos conos no converjan en el punto central del objeto, es inevitable que se presente una doble apariencia (Óptica, II, § 29); dicha doble apariencia desaparece cuando tapamos uno de los dos ojos.

Atendamos la figura 1.9, para aclarar la manera como Ptolomeo encara la visión binocular. Sean A y A′ la ubicación de dos ojos que han concentrado su atención en el punto D (sus ejes convergen en dicho punto). Sea EZ un objeto ubicado frontalmente ante los dos ojos. La definición de “ubicación frontal” debe perfeccionarse en relación con la que habíamos ofrecido para el caso de la visión monocular. Antes dijimos que un objeto se encuentra en disposición frontal en relación con un ojo si es perpendicular al eje del cono visual. Ahora bien, cuando el objeto es contemplado a partir de dos ejes, que de hecho no pueden ser paralelos si los ejes convergen en un punto del objeto, este no podrá disponerse en forma perpendicular a ambos ejes.

Figura 1.9. Visión binocular

Fuente: Elaboración del autor. La figura cuenta con modelación en el micrositio.

Ello exige definir otro eje de referencia para estipular la ubicación frontal. Sea CD el eje común de los dos conos visuales: D es el punto de convergencia de los ejes individuales y C es el punto medio de AA′. Así, el eje común nace en el punto medio entre los dos ojos, allí donde inicia el descenso de la nariz; dicho eje es perpendicular al segmento que une los dos ojos. Ptolomeo no ofrece ninguna justificación para la elección; entre tanto, los casos que analiza se restringen a imaginar D de tal manera que el eje común resulta perpendicular a AA′.44 En ese orden de ideas, un objeto se dispone frontalmente a dos ojos si es perpendicular al eje común. Así las cosas, todos los puntos individuales sobre el segmento EZ aparecerán, como mostramos a continuación, en una posición singular cada uno (Óptica, III, §§ 37-41). Algo muy diferente ocurre con los puntos T, H y K cuando son observados de tal modo que los ejes de los conos visuales convergen en D y no, por ejemplo, en T; tales puntos aparecen duplicados. Ptolomeo propuso un principio heurístico que estipula el lugar en donde se espera que un punto sea observado por un ojo cuando los dos ejes visuales convergen en un tercer punto (Óptica, III, § 36). El principio, sin embargo, no se deriva de una argumentación teórica previa que nos convenza de su plausibilidad. Se trata, más bien, de una conjetura, a la espera de verse justificada, si a partir de su aceptación hallamos explicaciones cualitativas sencillas de algunos fenómenos simples asociados con la percepción visual.

En forma resumida, el principio asevera que la ubicación aparente de un objeto puntual, cuando se contempla con los dos ojos, es tal que 1) la distancia de la imagen al eje común (el eje del cíclope) es igual a la distancia del objeto al eje visual del ojo que estemos considerando, siempre que dichas distancias se evalúen sobre la perpendicular al eje común trazada desde el objeto (Óptica, III, § 36); y 2) el lado en el que se observa la imagen con respecto al eje común es el mismo lado al que se observa con el ojo considerado.45 Si el principio es correcto, de un objeto singular podemos tener imágenes dobles (una para cada ojo) o una imagen singular (cuando las de los ojos independientes se funden en una sola).

Cuando T es observado por el ojo A atendiendo al eje AHD (dado que T se encuentra a la derecha del eje visual, a una distancia HT del eje central, medida sobre la perpendicular a CD que pasa por T), aparecerá, según el principio que quiere defender el autor, a la derecha del eje central, a una distancia TK igual a la distancia HT; en tanto que si es contemplado por el ojo A′ bajo el eje A′KD, aparecerá, aplicando el mismo principio, a la izquierda del eje central, en la posición H. Así, entonces, cuando usamos los dos ojos de manera simultánea, T será visto como una mancha en la posición K por el ojo A, y en la posición H, por el ojo A′ (Óptica, III, § 40). Ptolomeo introduce este principio heurístico sin justificación alguna y con la esperanza de verlo sustentado en las posibles explicaciones que se puedan derivar de él.

La confianza cualitativa en el principio se refuerza si pensamos que después de enfocar un objeto con nuestros dos ojos, procedemos alternativamente a contemplarlo, ora con el ojo derecho, ora con el izquierdo (cerrando primero el ojo izquierdo, luego el derecho); en esas circunstancias, observamos una imagen que se desplaza de izquierda a derecha y luego de nuevo a la izquierda.

El teorema de los parágrafos 48-49 (libro III) sintetiza el uso que Ptolomeo pretende dar al principio heurístico de la visión binocular. Citemos en extenso el teorema, que procedemos a analizar con base en la figura que hemos construido (véase figura 1.10):

Dejemos que el punto A represente el vértice de alguno de los conos visuales, y asumamos que CB es el eje común y que el eje visual AB interseque el eje común en el punto B. Tracemos la recta DEZH, y por los puntos D, E, H levantemos las perpendiculares a BC, DTK, EL y HNM. Construyamos DS = recta TK, unamos SL y extendámosla hasta intersecar la prolongación de NH en el punto I. Decimos, entonces, que DEH aparecerá al ojo en A como si estuviese a lo largo de SLI (Óptica, III, §§ 48-49).46

La idea de Ptolomeo es sencilla, aunque está formulada en un lenguaje complejo para nosotros. En la figura 1.10, A y A′ representan la ubicación de los ojos izquierdo y derecho; C, el punto medio entre los dos ojos —allí donde inicia el descenso de la nariz—. Este es el vértice de una nueva pirámide que resume la contribución de cada pirámide independiente, allí donde tendría que estar el ojo del cíclope. CB es perpendicular a AA′ y es el eje visual asociado a la nueva pirámide. JG representa un objeto dispuesto frontalmente (perpendicular al eje CB) y a la misma altura de los dos ojos, mientras B es el punto de dicho objeto sobre el cual convergen los ejes independientes AB y A′B.

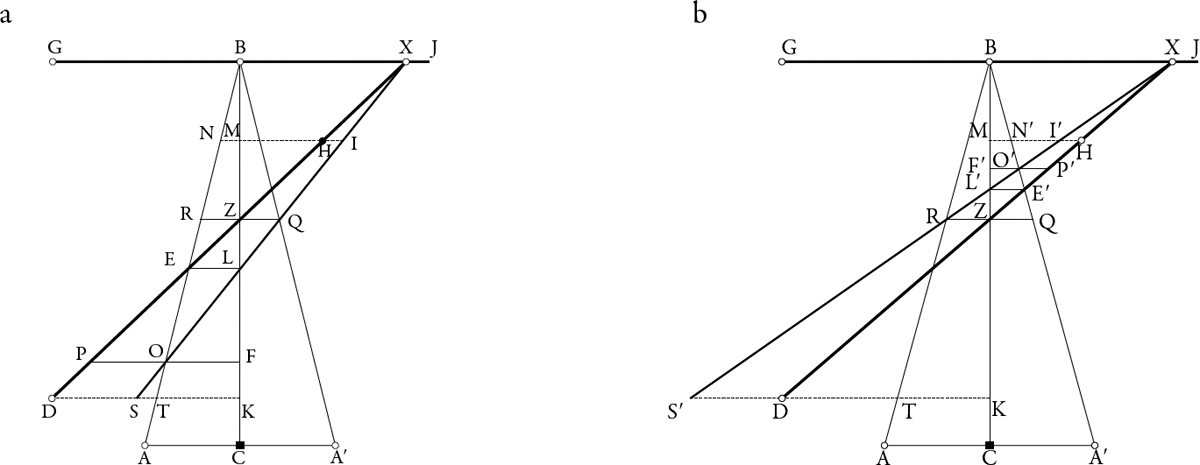
Figura 1.10. Principio heurístico a. Ojo izquierdo; b. ojo derecho

Fuente: Elaboración del autor. La figura cuenta con modelación en el micrositio.

Ptolomeo imagina que el observador fija su atención en B y por ello logra que los dos ejes independientes converjan en dicho punto. A continuación quiere saber qué tipo de imagen de los demás puntos cercanos percibimos con los dos ojos. Para ello, imagina un objeto recto dispuesto al frente del observador, en el mismo plano que contiene los puntos G, J, A y A′. Sea DX ese objeto. No es necesario que X forme parte de GJ. Ptolomeo quiere saber cómo es visto DX por cada uno de los dos ojos, siempre que la mirada esté fija en B y podamos darle crédito al principio heurístico propuesto.

Sea H un punto cualquiera de DX. El principio heurístico demanda que tracemos la perpendicular HM al eje común CB y determinemos el corte N con el eje del ojo izquierdo, AB (véase figura 1.10a), y el corte N′ con el eje del ojo derecho, A′B (véase figura 1.10b). A continuación debemos construir el segmento MI (ojo izquierdo) y MI′ (ojo derecho), de tal forma que MI ≅ NH y MI′ N′H. En la construcción hay que tener en cuenta que I y H están al mismo lado de CB y AB respectivamente, y que I′ y H están al mismo lado de CB y A′B respectivamente.

Si repetimos este procedimiento para cada uno de los puntos H que se distribuyen a lo largo de la recta DX, se puede probar, como lo hizo Ptolomeo, que los nuevos puntos I e I′ se distribuyen a lo largo de las rectas SX para el ojo izquierdo y S′X para el ojo derecho. En la demostración restringida al ojo izquierdo, Ptolomeo primero ubica S sobre DK, perpendicular a CB, de tal forma que S satisface el criterio heurístico para D. A continuación encuentra el punto de corte E de la recta DX con el eje del ojo izquierdo. Como la distancia de ese punto al eje es 0, la imagen de E, según el principio, debe hallarse en L sobre el eje CB.47 Ptolomeo prueba que cada uno de los puntos I de la recta SL satisface el principio heurístico para el punto correspondiente H.48